содержание .. 16 17 18 19 ..
Большая книга занимательных наук (Яков Перельман) - часть 18
Конечная строка первой из только что рассмотренных «пирамид» 12345678 x 9 + 9= 111111111
представляет образчик целой группы интересных арифметических курьезов, собранной в нашем музее в следующую таблицу:
12345679 × 9 = 111111111
12345679 × 18 = 222222222
12345679 × 27 = 333333333
12345679 × 36 = 444444444
12345679 × 45 = 555555555
12345679 × 54 = 666666666
12345679 × 63 = 777777777
12345679 × 72 = 888888888
12345679 × 81 = 999999999
Откуда такая закономерность в результатах? Примем во внимание, что
12345678 х 9 + 9 = (12345678 + 1) х 9 = 12345679 х 9.
Поэтому 12345679 x 9= 111111111.
А отсюда прямо следует, что 12345679 х 9 х 2 = 222222222
12345679 х 9 х 3 = 333333333
12345679 х 9 х 4 = 444444444 и т. д.
Любопытно, что получится, если число 111111111, с которым мы
сейчас имели дело, умножить само на себя? Заранее можно предвидеть, что результат должен быть диковинный, – но какой именно?
Если вы обладаете способностью четко рисовать в воображении ряды
цифр, вам удастся найти интересующий нас результат, даже не прибегая к выкладкам на бумаге. В сущности здесь дело сводится только к надлежащему расположению частных произведений, потому что умножать приходится все время лишь единицу на единицу – действие, могущее затруднить разве лишь фонвизинского Митрофанушку, размышлявшего о результате умножения «единожды один». Сложение же частных произведений сводится к простому счету единиц. Вот результат этого единственного в своем роде умножения (при выполнении которого не приходится нигде прибегать к действию умножения):
Все девять цифр выстроены в стройном порядке, симметрично убывая от середины в обе стороны.
Те из читателей, которых утомило обозрение числовых диковинок,
могут покинуть здесь эту галерею и перейти в следующие отделения, где показываются фокусы и выставлены числовые великаны и карлики; я хочу сказать: они могут прекратить чтение этой главы и обратиться к
дальнейшим. Но кто желает познакомиться еще с несколькими интересными достопримечательностями мира чисел, приглашаю осмотреть со мною несколько ближайших витрин.
Что за странные кольца выставлены в следующей витрине нашей
галереи?
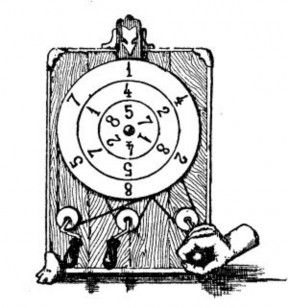
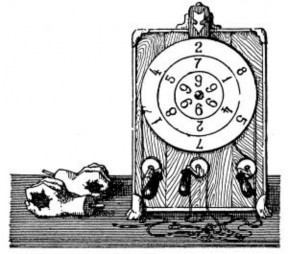
Перед нами три плоских кольца, вращающихся одно в другом (рис. 1).
На каждом кольце написаны шесть цифр в одном и том же порядке, именно
– обозначено число: 142857. Кольца обладают следующим удивительным свойством: как бы ни были они повернуты, мы при сложении двух написанных на них чисел, считая от любой цифры в направлении часовой стрелки, получим во всех случаях шестизначное число (если только результат вообще будет шестизначный), лишь немного подвинутое!
Рис. 1. Вращающиеся числовые кольца
В том, например, положении, какое изображено на прилагаемом
чертеже, мы получаем при сложении двух наружных колец:
т. е. опять тот же ряд цифр: 142857, только цифры 5 и 7 перенеслись из
конца в начало.
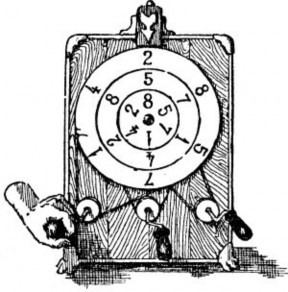
При другом расположении колец относительно друг друга (рис. 2) имеем такие случаи:
Рис. 2. Другое расположение колец
Исключение составляет случай, когда в результате получается 999999 (рис. 3):
(Причину других отступлений от указанного правила читатель поймет, когда дочитает эту статью до конца.)
Мало того. Тот же ряд цифр в той же последовательности мы получим и при вычитании чисел, написанных на кольцах.
Например:
Рис. 3. Исключение составляет случай, когда в результате получается 999999
Исключение составляет случай, когда приведены к совпадению одинаковые цифры; тогда, разумеется, разность равна нулю.
Но и это еще не все. Умножьте число 142857 на 2, на 3, на 4, на 5 или на 6 – и вы получите снова то же число, лишь передвинутое в круговом порядке на одну или несколько цифр:
142857 × 2 = 285714
142857 × 3 = 428571
142857 × 4 = 571428
142857 × 5 = 714285
142857 × 6 = 857142
Чем же все загадочные особенности нашего числа обусловлены?
Мы нападем на путь к разгадке, если продлим немного последнюю табличку и попробуем умножить наше число на 7: в результате получится 999999. Значит, число 142857 не что иное, как седьмая часть 999999; и,
следовательно, дробь
Действительно, если станете превращать 000/7 в десятичную дробь, вы получите:
Наше загадочное число есть период бесконечной периодической дроби, которая получается при превращении 000/7 в десятичную. Становится понятным теперь, почему при удвоении, утроении и т. д. этого числа
происходит лишь перестановка одной группы цифр на другое место. Ведь
умножение этого числа на 2 делает его равным 2/7 и, следовательно, равносильно превращению в десятичную дробь уже не 000/7, а 2/7. Начав же превращать дробь 2/7 в десятичную, вы сразу заметите, что цифра 2 – один из тех остатков, которые у нас уже получались при превращении 1/7; ясно, что должен повториться и прежний ряд цифр частного, но начнется он с
другой цифры. Иными словами, должен получиться тот же период, но только несколько начальных цифр его очутятся на конце. То же самое произойдет и при умножении на 3, на 4, на 5 и на 6, то есть на все числа, получающиеся в остатках. При умножении же на 7 мы должны получить единицу, или – что то же самое – 0,9999…
Любопытные результаты сложения и вычитания чисел на кольцах находят себе объяснение в том же факте, что 142857 есть период дроби,
равной 000/7. В самом деле: что мы собственно делаем, поворачивая кольцо на несколько цифр? Переставляем группу цифр с начала строки на конец, то есть согласно только что сказанному умножаем число 142857 на 2, на 3, на 4 и т. д. Следовательно, все действия сложения или вычитания чисел,
написанных на кольцах, сводятся к сложению или вычитанию дробей 000/7, 2/7, 3/7 и т. д. В результате мы должны получить, конечно, несколько
седьмых долей, то есть опять-таки наш ряд цифр 142857 в той или иной круговой перестановке. Отсюда надо исключить лишь случаи, когда складываются такие числа седьмых долей, которые в сумме дают единицу
или больше 1.
Но и последние случаи исключаются не вполне: они дают результат, правда, не тождественный с рассмотренными, но все же сходный с ними.
Рассмотрим внимательнее, что должно получиться от умножения нашего загадочного числа на множитель больше 7, то есть на 8, на 9 и т. д.
Умножить 142857, например, на 8 мы можем так: умножить сначала на 7 и
к произведению (то есть к 999999) прибавить наше число:
142857 х 8 = 142857 х 7 + 142857 = 999999 + 142857 = 1000000 – 1 +
142857 = 1000000 + (142857 – 1).
Окончательный результат – 1142856 – отличается от умножаемого 142857 только тем, что впереди стоит еще одна единица, а последняя цифра на единицу же уменьшена. По сходному правилу составляются произведения 142857 на всякое другое число больше 7, как легко усмотреть из следующих строк:
142807 х 8 = (142857 х 7) + 142857 = 1000000 – 1 + 142857 = 1142856
142857 х 9 = (142857 х 7) + (142857 х 2) = 1000000 – 1 +285714=
1285713
142857 х 10 = (142857 х 7) + (142857 х 3) = 1000000 – 1 +428571 =
1428570
142857 х 16 = (142857 х 7 х 2) + (142857 х 2) = 2000000 -2 + 285714 =
2285713
142857 х 39 = (142857 х 7 х 5) + (142857 х 4) = 5000000 -5 + 571428 =
5571427
Общее правило здесь такое: при умножении 142857 на любой множитель нужно умножить лишь на остаток от деления множителя на 7; впереди этого произведения ставится число, показывающее, сколько семерок в множителе, и то же число вычитается из результата[68]. Пусть мы желаем умножить 142857 на 88. Множитель 88 при делении на 7 дает в частном 12 и в остатке 4. Следовательно, результат умножения таков:
12 571 428– 12 = 12 571 416.
От умножения 142857 на 365 мы получим (так как 365 при делении на 7 дает в частном 52, а в остатке 1):
52 142 857 – 52 = 52 142 805.
Усвоив это простое правило и запомнив результаты умножения нашего
диковинного числа на множители от 2 до 6 (что весьма нетрудно, нужно
помнить лишь, с какой цифры они начинаются), вы можете изумлять непосвященных молниеносным умножением шестизначного числа. А чтобы не забыть этого удивительного числа, заметим, что оно произошло
от 000/7, или, что то же самое, от 2/14; вот вам первые три цифры нашего числа: 142. Остальные три получаются вычитанием первых трех из 999:
Мы уже имели дело с такими числами – именно когда знакомились со
свойствами числа 999. Вспомнив сказанное там, мы сразу сообразим, что число 142857 есть, очевидно, результат умножения 143 на 999:
142 857 = 143 х 999.
Но 143 = 13 х 11. Припомнив замеченное раньше о числе 1001, равном 7 х 11 х 13, мы будем в состоянии, не выполняя действия, предсказать, что должно получиться от умножения 142857 х 7:
142857 х 7 = 143 х 999 х 7 = 999 х 11 х 13 х 7 = 999 х 1001 = 999 999
(все эти преобразования мы, конечно, можем проделать в уме).
Чисел, подобных тому, с которым мы познакомились, существует множество. Они составляют словно одно семейство, так как объединены
общим происхождением – от превращения простых дробей в бесконечные десятичные. Но не всякий период десятичной дроби обладает рассмотренным выше любопытным свойством давать при умножении круговую перестановку цифр. Не вдаваясь в тонкости теории, отметим, что это имеет место только для тех дробей, число цифр периода которых на единицу меньше знаменателя соответствующей простой дроби. Так,
например:
000/7 дает в периоде 6 цифр. 1/17»»» 16»
000/19»»» 18»
000/23»»» 22»
Вы можете убедиться испытанием, что периоды дробей,
получающихся от превращения 000/17,1/19,1/23 и 1 /29 в десятичные, обладают теми же особенностями, как и рассмотренный нами период дроби 1/7.
Например, от 000/29 получаем число
0 344 827 586 206 896 551 724 137 931.
Если указанное сейчас условие (относительно чисел цифр периода) не соблюдено, то соответствующий период дает число, не принадлежащее к занимающей нас семье интересных чисел. Например, 000/13 дает десятичную дробь с шестью (а не с 12) цифрами в периоде:
000/13 = 0,076923.
Помножив на 2, получаем совершенно иное число: 2/13 = 0,153846.
Почему? Потому что среди остатков от деления 1:13 не было числа 2.
Различных остатков было столько, сколько цифр в периоде, то есть 6;
различных же множителей для дроби 000/13 у нас 12; следовательно, не все множители будут среди остатков, а только 6. Легко убедиться, что эти
множители следующие: 1, 3,4, 9,10, 12. Умножение на эти 6 чисел дает
круговую перестановку (076 923 х 3 = 230 769), на остальные – нет. Вот почему от 000/13 получается число, лишь отчасти пригодное для
«магического кольца». То же надо сказать и о ряде других периодов.
В 1916 году, в разгар империалистической войны, некоторые газеты нейтральной Швейцарии занимались арифметическим «гаданием» о… грядущей судьбе императоров Германии и Австрии. «Пророки» складывали следующие столбцы чисел:
Для Вильгельма II:
Для Франца-Иосифа:
В совпадении сумм «пророки» видели мрачное предзнаменование для коронованных особ, и так как каждый итог представлял собой удвоенный 1916 год, то обоим императорам предрекали гибель именно в этом году.
Между тем совпадение результатов с математической стороны не
является неожиданным. Стоит немного изменить порядок слагаемых – и станет понятно, почему они дают в итоге удвоенный 1916 год. В самом
деле, разместим слагаемые так:
год рождения, возраст,
год вступления на престол, число лет царствования.
Что должно получиться, если к году рождения прибавить возраст?
Разумеется, дата того года, когда производится вычисление. Точно так же, если к году вступления на престол прибавить число лет царствования,
получится опять год, когда производится расчет. Ясно, что итог сложения
четырех наших слагаемых может быть не чем иным, как удвоенным годом выполнения расчета. Очевидно, судьба императоров абсолютно не зависит от подобной арифметики…
Так как о сказанном выше не все догадываются, то можно воспользоваться этим для забавного арифметического фокуса. Предложите кому-нибудь написать тайно от вас четыре числа:
год рождения,
год поступления в школу (на завод и т. п.), возраст,
число лет обучения в школе (работы на заводе и т. п.).
Вы беретесь отгадать сумму этих чисел, хотя ни одно из них вам не известно. Для этого вы удваиваете год выполнения фокуса и объявляете итог. (Если, например, фокус показывается в 1954 году, то сумма – 3908.)
Чтобы иметь возможность, не обнаруживая секрета, с успехом проделывать этот фокус несколько раз подряд, вы заставляете слушателя проводить над суммой какие-нибудь арифметические действия, маскируя
этим свой прием.
Из многочисленных разновидностей фокусов этого рода опишем один, основанный на знакомом уже нам свойстве множителя, состоящего из ряда одних девяток; когда умножают на него число со столькими же цифрами, получается результат, состоящий из двух половин: первая – это
умножаемое число, уменьшенное на единицу; вторая – результат вычитания первой половины из множителя. Например: 247 х 999 = 246 753;
1372 х 999 = 13 718 628 и т. д. Причину легко усмотреть из следующей
строки:
247 х 999 = 247 х (1000 – 1) = 247 000–247 = 246 999–246.
Пользуясь этим, вы предлагаете группе товарищей произвести деление
многозначных чисел:
одному – 68 933 106: 6894,
другому – 8 765 112 348: 9999,
третьему – 543 456: 544,
четвертому – 12 948 705: 1295 и т. д.,
а сами беретесь обогнать их всех, выполняя те же задачи. И прежде
чем они успеют приняться за дело, вы уже вручаете каждому бумажку с полученным вами безошибочным результатом деления:
первому – 9999,
второму – 87 652,
третьему – 999,
четвертому – 9999.
Вы можете сами придумать по указанному образцу ряд других способов поражать непосвященных мгновенным выполнением деления: для этого воспользуйтесь некоторыми свойствами тех чисел, которые
помещены в «Галерее числовых диковинок».
Попросите кого-нибудь сообщить вам любимую его цифру. Допустим, вам назвали цифру 6.
Вот удивительно! – восклицаете вы. – Да ведь это как раз самая замечательная из всех значащих цифр.
Чем же она замечательна? – осведомляется заинтересованный собеседник.
Вот посмотрите: умножьте вашу любимую цифру на число значащих цифр, то есть на 9, и полученное число (54) подпишите множителем под числом 12 345 679:
Что получится в произведении?
Ваш собеседник выполняет умножение – и с изумлением получает
результат, состоящий сплошь из его любимых цифр: 666 666 666.
Видите, какой у вас тонкий арифметический вкус, – заканчиваете
вы. – Вы сумели избрать из всех цифр как раз ту, которая обладает столь замечательным свойством!
Однако в чем тут дело?
Точно такой же изысканный вкус оказался бы у вашего собеседника, если бы он избрал какую угодно другую из девяти значащих цифр, потому что каждая из них обладает тем же свойством:
Почему это так, вы сообразите, если припомните то, что говорилось о числе 12 345 679 в «Галерее числовых диковинок».
Фокусы, относящиеся к этой категории, могут быть изменяемы на разные лады.
Опишу один из видов этого фокуса, довольно сложный, но именно
потому и производящий сильное впечатление.
Допустим, что вы родились 18 мая и что вам теперь 23 полных года. Я, конечно, не знаю ни даты вашего рождения, ни вашего возраста. Тем не менее я берусь отгадать то и другое, заставив вас проделать лишь некоторый ряд вычислений.
А именно: порядковый номер месяца (май, 5-й месяц) я прошу вас умножить на 100, прибавить к произведению число месяца (18), сумму удвоить, к результату прибавить 8, полученное число умножить на 5, к произведению прибавить 4, помножить результат на 10, прибавить 4 и к полученному числу прибавить ваш возраст (23).
Когда вы все это проделаете, вы сообщаете мне окончательный результат вычислений. Я вычитаю из него 444, а разность разбиваю на
грани, справа налево, по две цифры в каждой: получаю сразу как месяц и число вашего рождения, так и ваш возраст.
Действительно. Проделаем последовательно все указанные вычисления:
5 × 100 = 500
500 + 18 = 518
518 × 2 = 1036
1036 + 8 = 1044
1044 × 5 = 5220
5220 + 4 = 5224
5224 × 10 = 52240
52240 + 4 = 52244
52244 + 20 = 52264
Произведя вычитание 52 267–444, получаем число 51 823.
Теперь разобьем это число на грани, справа налево, по две цифры в каждой. Имеем:
5-18-23,
то есть 5-го месяца (мая), числа 18; возраст 23 года. Почему же так получилось?
Секрет наш легко понять из рассмотрения следующего равенства:
{[(100 т + t) х 2 + 8] х 5 + 4} х 10 + 4 + n – 444 = 10000m +100t +
п.
Здесь буква т обозначает порядковый номер месяца, t – число месяца, п – возраст. Левая часть равенства выражает все последовательно
произведенные вами действия, а правая – то, что должно получиться, если раскрыть скобки и проделать возможные упрощения.
В выражении 10000 т + 100t + п ни т, ни t, ни п не могут быть более чем двузначными числами; поэтому число, получающееся в результате, всегда должно при делении на грани, по две цифры в каждой, расчлениться на три части, выраженные искомыми числами m,t и
n.
Предоставляем изобретательности читателя придумать видоизменения фокуса, то есть другие комбинации действий, дающие подобный же результат.
В заключение, ничего у вас не спрашивая, я отгадаю результат, который вы получите в итоге выкладок над задуманным вами числом.
Задумайте любую цифру, кроме ноля. Умножьте ее на 37. Полученное умножьте на 3. Последнюю цифру произведения зачеркните, а оставшееся число разделите на первоначально задуманную цифру; остатка не будет.
Я могу сказать вам, какое число вы получили, хотя все это я написал задолго до того, как вы приступили к чтению книги.
У вас получилось число 11.
Второй раз проделаем фокус на иной лад. Задумайте двузначное число. Припишите к нему справа то же число еще раз. Полученное четырехзначное число разделите на то, которое вы первоначально
задумали: деление выполнится нацело. Все цифры частного сложите.
У вас получилось 2.
Если не так, то проверьте внимательно свои вычисления и убедитесь,
что ошиблись вы, а не я.
В чем разгадка этих фокусов?
Наш читатель теперь достаточно уже опытен в разгадывании фокусов и не потребует от меня долгих объяснений. В первом опыте отгадывания задуманное число умножалось сначала на 37, потом на 3. Но 37x3 = 111,а умножить цифру 111 – значит составить число из трех таких же одинаковых цифр (например, 4 х 37 х 3 = 444). Что мы проделали далее? Мы зачеркнули последнюю цифру и, следовательно, получили число из двух одинаковых цифр (44), которое, конечно, должно делиться на задуманную цифру и дать в частном 11.
Во втором опыте задуманное двузначное число мы писали дважды кряду – например, задумав 29, писали 2929. Это все равно, что умножить задуманное число на 101 (в самом деле, 29 х 101 = 2929). Раз я это знаю, я могу с уверенностью предвидеть, что от деления такого четырехзначного числа на задуманное число получится 101 и что, следовательно, сумма цифр частного (1+0+1) равна 2.
Как видите, отгадывание основано на свойствах чисел 111 и 101; мы вправе поместить оба эти числа в нашу арифметическую кунсткамеру.
Высочайшая пирамида древнего Египта – Хеопсова, уже пять тысячелетий обвеваемая знойным воздухом пустыни, представляет, без сомнения, самую удивительную постройку, сохранившуюся от Древнего
мира. Высотой почти в 150 м, она покрывает своим основанием площадь в 40 000 кв. м и сложена из 200 рядов исполинских камней. 10 000 рабов в течение 30 лет трудились над возведением этого сооружения, сначала
подготовляя 10 лет дорогу для перевозки камней от каменоломни до места постройки, а затем громоздя их
20 лет друг на друга с помощью несовершенных машин того времени.
Было бы странно, чтобы такое огромное сооружение воздвигнуто было с единственной целью – служить гробницей для правителя страны. Поэтому некоторые исследователи стали доискиваться: не раскроется ли
тайна пирамиды из соотношения ее размеров?
Им посчастливилось, по их мнению, найти ряд удивительных соотношений, свидетельствующих о том, что жрецы, руководители работ
по постройке, обладали глубокими познаниями по математике и
астрономии и эти познания воплотили в каменных формах пирамиды.
«Геродот[69]
рассказывает, – читаем мы в книге французского астронома Море («Загадки науки», 1926, т. 1), – что египетские жрецы открыли ему следующее соотношение между стороной основания пирамиды и ее высотой: квадрат, построенный на высоте пирамиды, в точности равен площади каждого из боковых треугольников. Это вполне подтверждается новейшими измерениями. Вот доказательство, что во все времена пирамида Хеопса рассматривалась как памятник, пропорции которого рассчитаны математически.
Приведу более позднее доказательство: мы знаем, что отношение между длиной окружности и ее диаметром есть постоянная величина,
хорошо известная современным школьникам. Чтобы вычислить длину окружности, достаточно умножить ее диаметр на 3,1416.
Математики древности знали это отношение лишь грубо приближенно.
Но вот, если сложить четыре стороны основания пирамиды, мы получим для ее обвода 931,22 м. Разделив же это число на удвоенную
высоту (2 х 148,208), имеем в результате 3,1416, то есть отношение длины окружности к диаметру[70].
Еще удивительнее другое соотношение: если сторону основания пирамиды разделить на точную длину года – 365,2422 суток, то получается как раз 10000000-я доля земной полуоси – с точностью, которой могли бы
позавидовать современные астрономы…
Далее: высота пирамиды составляет ровно миллиардную долю расстояния от Земли до Солнца – величины, которая европейской науке
стала известна лишь в конце XVIII века. Египтяне 5000 лет назад знали, оказывается, то, чего не знали еще ни современники Галилея и Кеплера, ни ученые эпохи Ньютона. Неудивительно, что изыскания этого рода
породили на Западе обширную литературу.
А между тем все это – не более как игра цифрами. Дело представится
совсем в другом свете, если подойти к нему с оценкой результатов приближенных вычислений.
Рассмотрим же по порядку те примеры, которые мы привели.
О числе «пи». Арифметика приближенных чисел утверждает, что если в результате действия деления желаем получить число с шестью верными цифрами (3,14159), мы должны иметь в делимом и делителе по крайней мере столько же верных цифр. Это значит – в применении к пирамиде, – что для получения шестизначного «пи» надо было измерить стороны основания и высоту пирамиды с точностью до миллионных долей результата, то есть до 1 мм. Астроном Море приводит для высоты пирамиды 148,208 м, на первый взгляд как будто действительно с
точностью до 1 мм.
Но кто поручится за такую точность измерения пирамиды? Вспомним, что в лабораториях Института мер (ВИМС), где производятся точнейшие в мире измерения, не могут при измерении длины добиться такой точности (получают при измерении длины лишь шесть верных цифр). Понятно, насколько грубее может быть выполнено измерение каменной громады в
пустыне. Правда, при точнейших землемерных работах (при измерении так называемых «базисов») можно и на местности достичь такой же точности, как и в лаборатории, то есть ручаться за шесть десятичных знаков. Но, конечно, невозможно осуществить это в условиях измерения пирамиды. К тому же истинных, первоначальных размеров пирамиды давно нет в натуре, так как облицовка сооружения выветрилась, и никто не знает, какой
она была толщины. Чтобы быть добросовестным, надо брать размеры пирамиды в целых метрах, а тогда получается довольно грубое «пи», не более точное, чем то, которое давно известно из математического папируса Ринда.
Если пирамида действительно есть каменное воплощение числа «пи», то воплощение это, как видим, далеко не совершенное. Но вполне допустимо, что пирамида не сооружена ради выражения именно этого соотношения. В пределы приближенных трехзначных чисел для размеров пирамиды хорошо укладываются и другие допущения. Возможно,
например, что для высоты пирамиды было взято 2/3 ребра пирамиды или 2/3 диагонали ее основания. Вполне допустимо и то соотношение, которое было указано Геродотом: что высота пирамиды есть квадратный корень из площади боковой грани. Все это – догадки, столь же вероятные, как и
«гипотеза пи».
Следующее утверждение касается продолжительности года и длины
земного радиуса: если разделить сторону основания пирамиды на точную
длину года (число из семи цифр), то получим в точности 10000000-ю долю земной оси (число из пяти цифр). Но раз мы уже знаем, что в делимом у нас не больше трех верных цифр, то ясно, какую цену имеют здесь эти семь и пять знаков в делителе и в частном. Арифметика может ручаться в этом случае только за три цифры в длине года и земного радиуса. Год в 365 суток и земной радиус около 6400 км – вот числа, о которых мы вправе здесь говорить.
Что же касается расстояния от Земли до Солнца, то здесь недоразумение иного рода. Странно даже, как приверженцы теории могут не замечать допускаемой ими здесь логической ошибки. Ведь если, как они
утверждают, сторона пирамиды составляет известную долю земного радиуса, а высота – известную долю основания, то нельзя уже говорить, будто та же высота составляет определенную долю расстояния до Солнца. Что-нибудь одно – либо то, либо другое. А если случайно тут обнаруживается любопытное соответствие обеих длин, то оно всегда существовало в нашей планетной системе, и никакой заслуги жрецов в
этом быть не может.
Сторонники рассматриваемой теории идут еще далее: они утверждают, что масса пирамиды составляет ровно одну тысячебиллионную долю массы земного шара. Это соотношение, по их мнению, не может быть случайным и свидетельствует о том, что древнеегипетские жрецы знали не только геометрические размеры нашей планеты, но и задолго до Ньютона и
Кавендиша исчислили ее массу – «взвесили» земной шар.
Здесь та же самая нелогичность, что и в примере с расстоянием от Земли до Солнца. Совершенно нелепо говорить о том, будто масса пирамиды «выбрана» в определенном соответствии с массой земного шара. Масса пирамиды определилась с того момента, как назначены были размеры ее основания и высоты.
Нельзя одновременно сообразовать высоту пирамиды с основанием, составляющим определенную долю земного радиуса, и независимо от этого ставить ее массу в связь с массой Земли. Одно определяется другим.
Значит, должны быть отвергнуты всякие домыслы о знании египтянами массы земного шара. Это не более как числовая эквилибристика (то есть изворотливость).
Искусно оперируя с числами, опираясь на случайные совпадения,
можно доказать, пожалуй, все что угодно.
Мы видим, на каких шатких основаниях покоится легенда о непостижимой учености жрецов-архитекторов пирамиды.
Попутно мы имеем тут и маленькую наглядную демонстрацию пользы
того отдела арифметики, который занимается приближенными числами.
содержание ..
16
17
18
19 ..
Девять одинаковых цифр
Цифровая лестница

Магические кольца
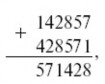
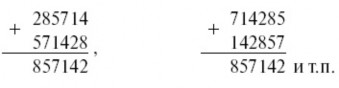

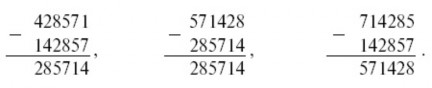
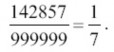

![]()

Мнимая неожиданность


Мгновенное деление
Любимая цифра
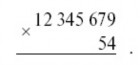
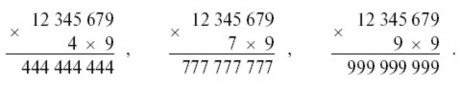
Угадать дату рождения
Отгадывание чисел
Математические загадки пирамиды Хеопса
![]()
![]()
![]()