содержание .. 17 18 19 20 ..
Большая книга занимательных наук (Яков Перельман) - часть 19
Для тех, кто не отдает себе достаточно ясного отчета в огромности миллиона и миллиарда, остаются не вполне осознанными колоссальные достижения нашего социалистического строительства, выражающиеся миллионными и миллиардными числами.
Чтобы ощутить грандиозность подобных чисел, стоит затратить немного времени на «арифметическую гимнастику», развивающую способность правильно оценивать подлинные размеры больших чисел.
Если хотите ощутить истинные размеры миллиона, попробуйте хотя бы проставить в чистой тетради миллион точек. Я не предлагаю вам доводить такую работу до конца (едва ли у кого на это хватит терпения); уже одно начало работы, медленный ее ход дадут вам почувствовать, что такое «настоящий» миллион.
Здесь я предлагаю доступный для каждого способ развить в себе возможно отчетливое представление о величине миллиона. Для этого нужно дать себе труд поупражняться в мысленном миллионном счете мелких, но хорошо знакомых нам единиц – шагов, минут, спичек, стаканов и т. п. Результаты получаются нередко неожиданные и поразительные.
Приведем несколько примеров.
Сколько времени отняла бы у вас работа – пересчитать миллион каких- либо предметов, по одному в каждую секунду?
Оказывается, что, считая безостановочно по 10 часов в сутки, вы
закончили бы подсчет в месяц времени! Приблизительно удостовериться в этом нетрудно устным вычислением: в часе 3600 секунд, в 10 часах – 36 000; в трое суток вы, следовательно, пересчитаете всего около 100 000
предметов; а так как миллион в 10 раз больше, то, чтобы досчитать до него, понадобится 30 дней[73]. Отсюда следует, между прочим, что предложенная ранее работа – поставить в тетради миллион точек – потребовала бы
многих недель самого усердного и неустанного труда.
Тонкость волоса вошла чуть не в поговорку. Все часто видят волос и хорошо знают, насколько он тонок.
Толщина человеческого волоса – около 0,07 мм. Мы округлим ее для удобства вычислений до 0,1 мм. Представьте себе, что рядом, бок о бок, положен миллион волос. Какой ширины получилась бы полоса? Можно ли было бы, например, протянуть ее поперек двери от косяка до косяка?
Если вы никогда не задумывались над такой задачей, то можно поручиться, что, не проделав вычисления, вы дадите грубо ошибочный ответ. Вы будете, пожалуй, даже оспаривать правильный ответ – настолько покажется он неправдоподобным. Каков же он?
Оказывается, что волос, увеличенный по толщине в миллион раз, имел
бы около сотни метров в поперечнике! Это кажется невероятным, но дайте себе труд сделать подсчет, и вы убедитесь, что так и есть:
0,1 мм х 1 000 000 = 0,1 м х 1000 = 0,1 км = 100 м.
Проделайте – лучше всего устно – еще ряд упражнений, чтобы освоиться надлежащим образом с величиной миллиона.
Величина обыкновенной комнатной мухи общеизвестна – около 7 мм в длину. Но какова была бы ее длина при увеличении в миллион раз?
РЕШЕНИЕ
Умножим 7 мм на 1 000 000, получим 7 км – примерно ширина Москвы или Ленинграда. Значит, муха, увеличенная линейно в миллион раз, могла бы покрыть своим телом столичный город!
Увеличьте мысленно в миллион раз (по ширине) ваши карманные
часы – и получите снова поражающий результат (едва ли вам удастся предугадать его без расчета). Какой?
РЕШЕНИЕ
Часы имели бы в ширину километров 50, а каждая цифра простиралась бы на географическую милю (7 км).
Какого роста достигал бы человек, увеличенный в миллион раз?
РЕШЕНИЕ
1700 километров! Он был бы всего в 8 раз меньше поперечника
земного шара. Буквально одним шагом мог бы он перешагнуть из
Ленинграда в Москву, а если бы лег, то растянулся бы от Финского залива до Крыма…
Приведу еще несколько готовых подсчетов того же рода, предоставляя
проверку их читателю.
Миллион человек, выстроенных в одну шеренгу плечом к плечу, растянулись бы на 250 км.
Миллион точек типографского шрифта – например, этой книги, – поставленных рядом вплотную, вытянулись бы в линию длиной в сотни метров.
Зачерпывая миллион раз наперстком, вы вычерпаете около тонны воды.
Книга в миллион страниц имела бы в толщину метров 50.
Миллион букв заключает книга убористой печати в 600–800 страниц среднего формата.
Миллион дней – более 27 столетий. От начала нашей эры не прошло
еще миллиона дней!
Миллиард – самое молодое из названий чисел. Оно вошло в употребление лишь со времени окончания франко-прусской войны (1871 год), когда французам пришлось уплатить Германии контрибуцию в 5 000 000 000 франков. Как и «миллион», слово «миллиард» происходит от корня
тысяча – и представляет собой итальянское увеличительное от этого существительного.
Чтобы составить себе представление об огромности миллиардов,
подумайте о том, что в книжке, которую вы сейчас читаете, заключается немногим более 200 000 букв. В пяти таких книжках окажется миллион букв. А миллиард букв будет заключать в себе стопка из 5000 экземпляров
этой книжки – стопка, которая, будучи аккуратно сложена, составила бы столб высотой с Исаакиевский собор (его высота – 101,52 м – примерно два с половиной шестнадцатиэтажных дома, поставленных друг на друга. –
Ред
).
В 1 куб. м содержится кубических миллиметров ровно миллиард (1000 х 1000 х 1000). Попробуем подсчитать, какой высоты получился бы столб,
если бы все эти крошечные миллиметровые кубики были поставлены один
на другой. Итог получается поразительный – 1000 км!
Миллиард минут составляет более 19 столетий; человечество всего 50 с лишним лет назад начало считать второй миллиард минут от первого дня нашей эры.
Гулливер в своих странствованиях, покинув карликов-лилипутов, очутился среди великанов. Мы путешествуем в обратном порядке: познакомившись с числовыми исполинами, переходим к миру лилипутов – к числам, которые во столько же раз меньше единицы, во сколько единица меньше арифметического великана.
Разыскать представителей этого мира не составляет никакого труда: для этого достаточно написать ряд чисел, обратных миллиону, миллиарду, биллиону и т. д., то есть делить единицу на эти числа. Получающиеся дроби
есть типичные числовые лилипуты, такие же пигмеи по сравнению с единицей, каким является единица по сравнению с миллионом,
миллиардом, биллионом и прочими числовыми исполинами.
Вы видите, что каждому числу-исполину соответствует число-лилипут и что, следовательно, числовых лилипутов существует не меньше, чем исполинов. Для них также придуман сокращенный способ обозначения. Мы уже упоминали, что весьма большие числа в научных сочинениях (по астрономии, физике) обозначаются так:
1 000 000……………….106
10 000 000……………….107
400 000 000……………..4 · 108
6 квадриллионов………..6 · 1015 и т. д.
Соответственно этому числовые лилипуты обозначаются следующим образом:
Есть ли, однако, реальная надобность в подобных дробях? Приходится ли когда-нибудь действительно иметь дело со столь мелкими долями единицы?
Об этом интересно побеседовать подробнее.
Секунда, по обычному представлению, – настолько малый промежуток времени, что с весьма мелкими частями ее не приходится иметь дела ни при каких обстоятельствах. Легко написать
секунды, но это чисто бумажная величина, потому что ничего будто бы не может произойти в такой ничтожный промежуток времени.
Так думают многие, но ошибаются, потому что в тысячную долю секунды могут успеть совершиться весьма многие явления.
Поезд, проходящий 36 км в час, делает в секунду 10 м и,
следовательно, в течение 1000-й доли секунды успевает продвинуться на сантиметр. Звук в воздухе переносится в течение 1000-й доли секунды на 33 см, а пуля, покидающая ружейный ствол со скоростью 700–800 м в
секунду, переносится за тот же промежуток времени на 70 см. Земной шар перемещается каждую 1000-ю долю секунды, в своем обращении вокруг Солнца, на 30 м. Струна, издающая высокий тон, делает в 1000-ю долю
секунды два-четыре и более полных колебания; даже комар успевает в это время взмахнуть вверх или вниз своими крылышками. Молния длится
гораздо меньше 1000-й доли секунды: в течение этого промежутка времени успевает возникнуть и прекратиться столь значительное явление природы
(молния простирается в длину на целые километры).
Но – возразите вы – 1000-ю долю секунды еще нельзя признать за лилипута, как никто не назовет тысячу числовым гигантом. Вот если взять миллионную долю секунды, то уж наверное можно утверждать, что это величина нереальная – промежуток времени, в течение которого ничего произойти не может. Ошибаетесь! Даже и одна 1 000 000-я доля секунды – для современного физика, например, – вовсе не чрезмерно маленький промежуток. В области явлений световых (и электрических) ученому сплошь и рядом приходится иметь дело с гораздо более мелкими частями секунды. Напомним прежде всего, что световой луч пробегает ежесекундно (в пустоте) 300 000 км; следовательно, в 1 000 000-ю долю секунды свет
успевает перенестись на расстояние 300 м – примерно на столько же, на сколько переносится в воздухе звук в течение целой секунды.
Далее: свет есть явление волнообразное, и число световых волн, минующих ежесекундно каждую точку пространства, исчисляется сотнями биллионов. Те световые волны, которые, действуя на наши глаза, вызывают ощущение красного света, имеют частоту колебаний 400 биллионов в
секунду; это значит, что в течение одной 1 000 000-й доли секунды в наш глаз вступает 400 миллионов волн, а одна волна вступает в глаз в течение 400 000 000 000 000-й доли секунды. Вот подлинный числовой лилипут!
Но этот несомненный, реально существующий лилипут является истинным великаном по сравнению с еще более мелкими долями секунды, с которыми физик встречается при изучении рентгеновых лучей. Эти
удивительные лучи, обладающие свойством проникать через многие непрозрачные тела, представляют собой, как и видимые лучи, волнообразное явление, но частота колебаний у них значительно больше, чем у видимых: она достигает 2500 биллионов в секунду. Волны следуют тут одна за другой в 60 раз чаще, чем в лучах видимого красного света. Значит, и в мире лилипутов существуют свои великаны и карлики. Гулливер был выше лилипутов всего в дюжину раз и казался им великаном. Здесь же один лилипут больше другого в пять дюжин раз и, следовательно, имеет право именоваться по отношению к нему исполином.
Интересно рассмотреть теперь, какие наименьшие расстояния приходится отмеривать и оценивать современным исследователям природы.
В метрической системе мер наименьшая единица длины для
обиходного употребления – миллиметр; он примерно вдвое меньше толщины спички. Чтобы измерять предметы, видимые простым глазом, такая единица длины достаточно мелка. Но для измерения бактерий и других мелких объектов, различимых только в сильные микроскопы, миллиметр чересчур крупен.
Ученые обращаются для таких измерений к более мелкой единице – микрону, который в 1000 раз меньше миллиметра. Так называемые красные кровяные тельца, которые насчитываются десятками миллионов в каждой капельке нашей крови, имеют в длину 7 микронов и в толщину 2 микрона. Стопка из 1000 таких телец имеет толщину спички.
Как ни мелок кажется нам микрон, он все же оказывается чрезмерно крупным для расстояний, которые приходится измерять современному физику. Мельчайшие, недоступные даже микроскопу частицы – молекулы, – из которых состоит вещество всех тел природы, и слагающие их еще более мелкие – атомы – имеют размеры от одной 100-й до одной 1000-й доли микрона. Если остановиться на последней величине, то и тогда
окажется, что миллион таких крупинок (а мы уже знаем, как велик миллион), будучи расположен на одной прямой, вплотную друг к другу, занял бы всего миллиметр.
Чтобы представить себе наглядную чрезвычайную малость атомов, обратимся к такой картине. Вообразите, что все предметы на земном шаре увеличились в миллион раз. Эйфелева башня в Париже (300 м высоты)
уходила бы тогда своей верхушкой на 300 000 км в мировое пространство и находилась бы в недалеком соседстве от орбиты Луны. Люди были бы величиной в 000/4 земного радиуса – в 1700 км; один шаг такого человека- гиганта унес бы его на 600–700 км. Мельчайшие красные тельца, миллиардами плавающие в его крови, имели бы каждое более 7 м в поперечнике. Волос имел бы 100 м в толщину. Мышь достигала бы 100 км в длину, муха – 7 км. Каких же размеров будет при таком чудовищном увеличении атом вещества?
Положительно не верится: его размеры предстанут пред вами в виде…
типографской точки шрифта этой книги!
Достигаем ли мы здесь крайних пределов пространственной малости, за которые не приходится переступать даже физику с его изощренными приемами измерений? Еще не особенно давно думали так; но теперь
установлено, что атом – целый мир, состоящий из гораздо более мелких
частиц и являющийся ареной действия могущественных сил. Например, атом водорода состоит из центрального ядра и быстро обращающегося
вокруг него электрона. Не входя в другие подробности, скажем только, что
поперечник электрона измеряется биллионными долями миллиметра. Другими словами, поперечник электрона почти в миллион раз меньше поперечника атома. Если же пожелаете сравнить размеры электрона с размерами пылинки, то расчет покажет вам, что электрон меньше пылинки примерно во столько же раз, во сколько пылинка меньше – чего бы вы думали? – земного шара!
Вы видите, что атом – лилипут среди лилипутов – является в то же время настоящим исполином по сравнению с электроном, входящим в его состав, – таким же исполином, каким вся Солнечная система является по отношению к земному шару.
Можно составить следующую поучительную лестницу, в которой каждая ступень является исполином по отношению к предыдущей ступени и лилипутом по отношению к последующей:
электрон атом пылинка дом
земной шар Солнечная система
расстояние до Полярной звезды Млечный Путь.
Каждый член этого ряда примерно в четверть миллиона раз больше
предыдущего и во столько же раз меньше последующего (имеются в виду линейные размеры (а не объемы), то есть поперечник атома, диаметр Солнечной системы, высота или длина дома и т. п.). Ничто не доказывает так красноречиво всю относительность понятий «большой» и «малый», как эта табличка. В природе нет безусловно большого или безусловно малого предмета. Каждая вещь может быть названа и подавляюще огромной и исчезающе малой, в зависимости от того, как на нее взглянуть, с чем ее сравнить.
Наши беседы о великанах и карликах из мира чисел были бы неполны,
если бы мы не рассказали читателю об одной изумительной диковинке этого рода – диковинке, правда, не новой, но стоящей дюжины новинок. Чтобы подойти к ней, начнем со следующей, на вид весьма незамысловатой
задачи:
Какое самое большое число можно написать тремя цифрами, не употребляя никаких знаков действия?
Хочется ответить: 999, – но, вероятно, вы уже подозреваете, что ответ другой, иначе задача была бы чересчур проста. И действительно, правильный ответ пишется так:
Выражение это означает: «девять в степени девять в девятой степени» (на языке математики такое выражение называется «третьей сверхстепенью девяти»). Другими словами: нужно составить произведение из стольких девяток, сколько единиц в результате умножения:
9 × 9 × 9 × 9 × 9 × 9 × 9 × 9 × 9.
Достаточно только начать вычисление, чтобы ощутить огромность предстоящего результата. Если у вас хватит терпения выполнить перемножение девяти девяток, вы получите число:
387 420 489.
Главная работа только начинается: теперь нужно найти
9387420489
то есть произведение 387 420 489 девяток. Придется сделать круглым счетом 400 миллионов умножений…
У вас, конечно, не будет времени довести до конца подобное вычисление. Но я лишен возможности сообщить вам готовый результат – по трем причинам, которые нельзя не признать уважительными. Во-
первых, число это никогда и никем еще не было вычислено (известен только приближенный результат). Во-вторых, если бы даже оно и было вычислено, то, чтобы напечатать его, понадобилось бы не менее тысячи таких книг, как эта, потому что число наше состоит из 369 693 061 цифры; набранное обыкновенным шрифтом, оно имело бы в длину 1000 км – от Ленинграда до Горького. Наконец, если бы меня снабдили достаточным количеством бумаги и чернил, я и тогда не мог бы удовлетворить вашего
любопытства. Вы легко можете сообразить почему: если я способен писать, скажем, без перерыва по две цифры в секунду, то в час я напишу 7200 цифр, а в сутки, работая непрерывно день и ночь, – не более 172 800 цифр.
Отсюда следует, что, не отрываясь ни на секунду от пера, трудясь круглые сутки изо дня в день без отдыха, я просидел бы за работой не менее 7 лет, прежде чем написал бы это число…
Могу сообщить вам, что это число начинается цифрами 428 124773
175 747 048 036 987 118 и кончается 89. Что находится между этим началом
и концом – неизвестно. А ведь там 369 693 061 цифра!..
Вы видите, что уже число цифр нашего результата невообразимо огромно. Как же велико само число, выражаемое этим длиннейшим рядом цифр? Трудно дать хотя бы приблизительное представление о его громадности, потому что такого множества вещей, считая даже каждый электрон за отдельную вещь, нет в целой Вселенной!
Архимед вычислил некогда, сколько песчинок заключал бы в себе мир, если бы весь он, до неподвижных звезд, наполнен был тончайшим песком. У него получился результат, не превышающий единицы с 63 нолями. Наше число состоит не из 64, а почти из 370 миллионов цифр – следовательно,
оно неизмеримо превышает огромное число Архимеда.
Поступим же по примеру Архимеда, но вместо «исчисления песчинок» произведем «исчисление электронов». Вы уже знаете, что электрон меньше песчинки примерно во столько же раз, во сколько раз песчинка меньше земного шара. Для радиуса видимой Вселенной примем расстояние в миллиард световых лет. Так как свет пробегает в секунду 300 000 км, а в
году 31 миллион секунд, то можно считать, что световой год равен круглым счетом 10 биллионам километров (гнаться за большей точностью здесь бесполезно). Значит, для радиуса всей известной нам Вселенной получаем величину 10 миллиардов биллионов километров, или, прибегая к способу изображения числовых великанов, объясненному раньше, 1022 км.
Объем шара такого радиуса можно вычислить по правилам геометрии:
он равен (с округлением) 44 · 1066 куб. км. Умножив это число на число кубических сантиметров в кубическом километре (1015), получим для объема видимой Вселенной величину 1081 куб. см (небезынтересно отметить, что Архимед в своем исчислении песчинок определял объем Вселенной в 5 · 1054 куб. см).
Теперь представим себе, что весь этот объем сплошь заполнен самыми тяжелыми из известных нам атомов – атомами элемента урана, которых идет на грамм около 1022 штук. Их поместилось бы в шаре указанного объема 10103 штуки. Дознано, что в каждом атоме урана содержится 238
электронов (внешних и внутренних). Поэтому во всей доступной нашему исследованию Вселенной могло бы поместиться не более 10106 электронов.
Число, состоящее «всего лишь» из 107 цифр… Как это мизерно по
сравнению с нашим числовым великаном почти из 370 миллионов цифр!
Вы видите, что, наполняя сплошь видимую Вселенную электронами, мы не исчерпали и небольшой доли того исполинского числа, которое
скромно скрывается под изображением:
Познакомившись с этим замаскированным гигантом, обратимся к его противоположности.
Соответствующий числовой лилипут получится, если разделим единицу на это число. Будем иметь:
что равно:
Мы имеем здесь знакомое нам огромное число в знаменателе.
Сверхвеликан превратился в сверхлилипута.
Необходимо сделать существенное замечание о великане из трех девяток. Я получил немало писем от читателей с утверждением, что выражение это вовсе не так трудно вычислить; ряд читателей даже
выполнили требуемый расчет, употребив на него сравнительно немного времени. Результат оказался несравненно скромнее того, о котором у меня рассказано. В самом деле, пишут они,
99= 387 420 489;
возвысив же 387 420 489 в 9-ю степень, получаем число «всего лишь» из 72 цифр. Это хотя и не мало, но до 370 миллионов цифр от него еще
очень далеко…
Читатели недоумевают, а между тем ошибка их в том, что ими неправильно понят смысл трехъярусного выражения из девяток. Они понимают его так:
в то время как правильное его понимание иное:
Отсюда огромная разница в итогах вычисления.
Оба способа понимания приводят к одинаковому результату только в
одном случае: когда мы имеем выражение
Тут безразлично, как вести вычисление: в обоих случаях получается один результат – 16.
Любопытно, что сейчас приведенное выражение вовсе не означает самого большого числа, какое можно изобразить тремя двойками. Можно получить гораздо большее число, если расположить двойки так:
22.
Это выражение равно 4 194 304, то есть значительно больше 16. Как видите, третья сверхстепень не во всех случаях выражает наибольшее число, какое можно изобразить тремя одинаковыми цифрами.
Белка на поляне
Сегодня утром я с белкой в прятки играл, – рассказывал во время завтрака один из собравшихся за столом дома отдыха. – Вы знаете в нашем лесу круглую полянку с одинокой березой посредине? За этим деревом и пряталась от меня белка. Выйдя из чащи на полянку, я сразу заметил беличью мордочку с живыми глазками, уставившуюся на меня из-за ствола.
Осторожно, не приближаясь, стал я обходить по краю полянки, чтобы взглянуть на зверька. Раза четыре обошел я дерево – но плутовка отступала по стволу в обратную сторону, по-прежнему показывая только мордочку. Так и не удалось мне обойти вокруг белки.
Однако, – возразил кто-то, – сами же вы говорите, что четыре раза обошли вокруг дерева.
Вокруг дерева, но не вокруг белки!
Но белка-то на дереве?
Что же из того?
То, что вы кружились и вокруг белки.
Хорошо кружился, если ни разу не видел ее спинки.
При чем тут спинка? Белка в центре, вы ходите по кругу, значит,
ходите вокруг белки.
Ничуть не значит. Вообразите, что я хожу около вас по кругу, а вы поворачиваетесь ко мне все время лицом, пряча спину. Скажете вы разве,
что я кружусь вокруг вас?
Конечно, скажу. Как же иначе?
Кружусь, хотя не бываю позади вас, не вижу вашей спины?
Далась вам спина! Вы замыкаете вокруг меня путь – вот в чем суть дела, а не в том, чтобы видеть спину.
Позвольте: что значит кружиться вокруг чего-нибудь? По-моему, это
означает только одно: становиться последовательно в такие места, чтобы
видеть предмет со всех сторон. Ведь правильно, профессор? – обратился
спорящий к сидевшему за столом старику.
Спор идет у вас в сущности о словах, – ответил ученый. – А в таких
случаях надо начинать всегда с того, о чем вы сейчас только завели речь: надо договориться о значении слов. Как понимать слова: «двигаться вокруг предмета»? Смысл их может быть двоякий. Можно, во-первых, разуметь под ними перемещение по замкнутой линии, внутри которой находится предмет. Это одно понимание. Другое: двигаться по отношению к предмету так, чтобы видеть его со всех сторон. Держась первого понимания, вы должны признать, что четыре раза обошли вокруг белки. Придерживаясь же второго, – обязаны заключить, что не обошли вокруг нее ни разу. Поводов для спора здесь, как видите, нет, если обе стороны говорят на одном языке, понимают слова одинаково.
Прекрасно, можно допустить двоякое понимание. Но какое все же правильнее?
Так ставить вопрос не приходится. Уславливаться можно о чем угодно. Уместно только спросить, что более согласно с общепринятым пониманием. Я сказал бы, что лучше вяжется с духом языка первое понимание и вот почему. Солнце, как известно, делает полный оборот
вокруг своей оси немного более, чем за 25 суток.
Солнце вертится?
Конечно, как и Земля вокруг оси. Вообразите, однако, что вращение Солнца совершается медленнее, а именно, что оно делает один оборот не в 25 суток, а в 365000/4 суток, т. е. в год. Тогда Солнце было бы обращено к Земле всегда одной и той же своей стороной; противоположной половины,
«спины» Солнца, мы никогда не видели бы. Но разве стал бы кто-нибудь утверждать из-за этого, что Земля не кружится вокруг Солнца?
Да, теперь ясно, что я все-таки кружился вокруг белки.
Есть предложение, товарищи! Не расходиться, – сказал один из слушавших спор. – Так как в дождь гулять никто не пойдет, а перестанет дождик, видно, не скоро, то давайте проведем здесь время за головоломками. Начало сделано. Пусть каждый по очереди придумает или припомнит какую-нибудь головоломку. Вы же, профессор, явитесь нашим верховным судьей.
Если головоломки будут с алгеброй или с геометрией, то я должна отказаться, – заявила молодая женщина.
И я тоже, – присоединился кто-то.
Нет, нет, участвовать должны все! А мы попросим присутствующих
не привлекать ни алгебры, ни геометрии, разве только самые начатки.
Возражений не имеется?
Тогда я согласна и готова первая предложить головоломку.
Прекрасно, просим! – донеслось с разных сторон. – Начинайте.
В коммунальной кухне
Головоломка моя зародилась в обстановке дачной квартиры. Задача, так сказать, бытовая. Жилица – назову ее для удобства Тройкиной – положила в общую плиту 3 полена своих дров, жилица Пятеркина – 5 полей, жилец Бестопливный, у которого, как вы догадываетесь, не было своих дров, получил от обеих гражданок разрешение сварить обед на общем огне. В возмещение расходов он уплатил соседкам 8 копеек. Как должны они поделить между собой эту плату?
Пополам, – поспешил заявить кто-то. Бестопливный пользовался их огнем в равной мере.
Ну, нет, – возразил другой, – надо принять в соображение, как участвовали в этом огне дровяные вложения гражданок. Кто дал 3 полена, должен получить 3 копейки; кто дал 5 полен – получает 5 копеек. Вот это будет справедливый дележ.
Товарищи, – взял слово тот, кто затеял игру и считался теперь председателем собрания. – Окончательные решения головоломок давайте
пока не объявлять. Пусть каждый еще подумает над ними. Правильные ответы судья огласит нам за ужином. Теперь следующий. Очередь за вами, товарищ пионер!
Работа школьных кружков
В нашей школе, – начал пионер, – имеется 5 кружков: слесарный, столярный, фотографический, шахматный и хоровой. Слесарный кружок
занимается через день, столярный – через 2 дня на 3-й, фотографический – каждый 4-й день, шахматный – каждый 5-й день и хоровой – каждый 6-й день. Первого января собрались в школе все 5 кружков, а затем занятия велись в назначенные по плану дни, без отступлений от расписания. Вопрос состоит в том, сколько в первом квартале было еще вечеров, когда собирались в школе все 5 кружков.
А год был простой или високосный? – осведомились у пионера.
Простой.
Значит, первый квартал – январь, февраль, март – надо считать за 90
дней?
Очевидно.
Позвольте к вопросу вашей головоломки присоединить еще один, – сказал профессор. – А именно: сколько в том же квартале года было таких
вечеров, когда кружковых занятий в школе вовсе не происходило?
Ага, понимаю! – раздался возглас. – Задача с подвохом. Ни одного дня не будет больше с 5 кружками и ни одного дня без всяких кружков. Это
уж ясно!
Почему? – спросил председатель.
Объяснить не могу, но чувствую, что отгадчика хотят поймать впросак.
Ну, это не довод. Вечером выяснится, правильно ли ваше предчувствие. За вами очередь, товарищ!
Кто больше?
Двое считали в течение часа всех, кто проходил мимо них на тротуаре. Один стоял у ворот дома, другой прохаживался взад и вперед по тротуару. Кто насчитал больше прохожих?
Идя, больше насчитаешь, ясное дело, – донеслось с другого конца
стола.
Ответ узнаем за ужином, – объявил председатель. – Следующий!
Дед и внук
То, о чем я скажу, происходило в 1932 г. Мне было тогда ровно столько лет, сколько выражают последние две цифры года моего рождения. Когда я об этом соотношении рассказал деду, он удивил меня заявлением,
что с его возрастом выходит то же самое. Мне это показалось невозможным…
Разумеется, невозможно, – вставил чей-то голос.
Представьте, что вполне возможно. Дед доказал мне это. Сколько же лет было каждому из нас?
Железнодорожные билеты
Я – железнодорожная кассирша, продаю билеты, – начала следующая участница игры. – Многим это кажется очень простым делом. Не подозревают, с каким большим числом билетов приходится иметь дело кассиру даже маленькой станции. Ведь необходимо, чтобы пассажиры могли получить билеты от данной станции до любой другой на той же дороге, притом в обоих направлениях. Я служу на дороге с 25 станциями. Сколько же, по-вашему, различных образцов билетов заготовлено железной дорогой для всех ее касс?
Ваша очередь, товарищ летчик, – провозгласил председатель.
Полет дирижабля
Из Ленинграда вылетел прямо на север дирижабль. Пролетев в северном направлении 500 км, он повернул на восток. Пролетев в эту сторону 500 км, дирижабль сделал новый поворот – на юг и прошел в
южном направлении 500 км. Затем он повернул на запад и, пролетев
500 км, опустился. Спрашивается: где расположено место спуска дирижабля относительно Ленинграда – к западу, к востоку, к северу или к
югу?
На простака рассчитываете, – сказал кто-то, – 500 шагов вперед, 500 вправо, 500 назад да 500 влево – куда придем? Откуда вышли, туда и придем!
Итак, где, по-вашему, спустился дирижабль?
На том же ленинградском аэродроме, откуда поднялся. Не так разве?
Именно не так.
В таком случае я ничего не понимаю!
В самом деле, здесь что-то неладно, – вступил в разговор сосед. – Разве дирижабль спустился не в Ленинграде?.. Нельзя ли повторить задачу?
Летчик охотно исполнил просьбу. Его внимательно выслушали и с
недоумением переглянулись.
Ладно, – объявил председатель. – До ужина успеем подумать об этой задаче, а сейчас будем продолжать.
Тень
Позвольте мне, – сказал очередной загадчик, – взять сюжетом головоломки тот же дирижабль. Что шире: дирижабль или его полная тень?
В этом и вся головоломка?
Вся.
Тень, конечно, шире дирижабля: ведь лучи солнца расходятся веером, – последовало сразу решение.
Я бы сказал, – возразил кто-то, – что, напротив, лучи солнца параллельны; тень и дирижабль одной ширины.
Что вы? Разве не случалось вам видеть расходящиеся лучи от спрятанного за облаком солнца? Тогда можно воочию убедиться, как сильно расходятся солнечные лучи. Тень дирижабля должна быть значительно больше дирижабля, как тень облака больше самого облака.
Почему же обычно принимают, что лучи солнца параллельны?
Моряки, астрономы – все так считают…
Председатель не дал спору разгореться и предоставил слово следующему загадчику.
Задача со спичками
Очередной оратор высыпал на стол все спички из коробка и стал распределять их в три кучки.
Костер собираетесь раскладывать? – шутили слушатели.
Головоломка, – объяснил загадчик, – будет со спичками. Вот их три
неравные кучки. Во всех вместе 48 штук. Сколько в каждой, я вам не
сообщаю. Зато отметьте следующее: если из первой кучи я переложу во вторую столько спичек, сколько в этой второй куче имелось, затем из
второй в третью переложу столько, сколько в этой третьей перед тем будет
находиться, и, наконец, из третьей переложу в первую столько спичек, сколько в этой первой куче будет тогда иметься, – если, говорю, все это проделать, то число спичек во всех кучках станет одинаково. Сколько же было в каждой кучке первоначально?
Коварный пень
Головоломка эта, – начал сосед последнего загадчика, – напоминает задачу, которую давно как-то задал мне деревенский математик. Это был целый рассказ, довольно забавный. Повстречал крестьянин в лесу незнакомого старика. Разговорились. Старик внимательно оглядел крестьянина и сказал:
Известен мне в леску этом пенечек один удивительный. Очень в нужде помогает.
Как помогает? Вылечивает?
Лечить не лечит, а деньги удваивает. Положишь под него кошель с деньгами, досчитаешь до ста – и готово: деньги, какие были в кошельке, удвоились. Такое свойство имеет. Замечательный пень!
Вот бы мне испробовать, – мечтательно сказал крестьянин.
Это можно. Отчего же? Заплатить только надо.
Кому платить? И много ли?
Тому платить, кто дорогу укажет. Мне, значит. А много ли, о том особый разговор.
Стали торговаться. Узнав, что у крестьянина в кошельке денег мало,
старик согласился получать после каждого удвоения по 1 р. 20 к. На том и порешили.
Старик повел крестьянина в глубь леса, долго бродил с ним и, наконец, разыскал в кустах старый, покрытый мохом еловый пень. Взяв из рук крестьянина кошелек, он засунул его между корнями пня. Досчитали до ста. Старик снова стал шарить и возиться у основания пня, наконец извлек оттуда кошелек и подал крестьянину.
Заглянул крестьянин в кошелек и что же? – деньги в самом деле удвоились! Отсчитал из них старику обещанные 1 p. 20 к. и попросил
засунуть кошелек вторично под чудодейственный пень.
Снова досчитали до ста, снова старик стал возиться в кустах у пня, и снова совершилось диво: деньги в кошельке удвоились. Старик вторично получил из кошелька обусловленные 1 р. 20 к.
В третий раз спрятали кошель под пень. Деньги удвоились и на этот
раз. Но когда крестьянин уплатил старику обещанное вознаграждение, в кошельке не осталось больше ни одной копейки. Бедняга потерял на этой
комбинации все свои деньги. Удваивать дальше было уже нечего, и
крестьянин уныло побрел из лесу.
Секрет волшебного удвоения денег вам, конечно, ясен: старик недаром, отыскивая кошелек, мешкал в зарослях у пня. Но можете ли вы ответить на другой вопрос: сколько было у крестьянина денег до злополучных опытов с коварным пнем?
Задача о декабре
Я, товарищи, языковед, от всякой математики далек, – начал пожилой человек, которому пришел черед задавать головоломку. – Не ждите от меня поэтому математической задачи. Могу только предложить вопрос из знакомой мне области. Разрешите задать календарную головоломку?
Просим!
Двенадцатый месяц называется у нас «декабрь». А вы знаете, что, собственно, значит «декабрь»? Слово это происходит от греческого слова
«дека» – десять, отсюда также слово «декалитр» – десять литров, «декада»
десять дней и др. Выходит, что месяц декабрь носит название «десятый». Чем объяснить такое несоответствие?
Ну теперь осталась только одна головоломка, – произнес председатель.
Арифметический фокус
Мне приходится выступать последним, двенадцатым. Для разнообразия покажу вам арифметический фокус и попрошу раскрыть его секрет. Пусть кто-нибудь из вас, хотя бы вы, товарищ председатель,
напишет на бумажке, тайно от меня, любое трехзначное число.
Могут быть и нули в этом числе?
Не ставлю никаких ограничений. Любое трехзначное число, какое пожелаете.
Написал. Что теперь?
Припишите к нему это же число еще раз. У вас получится, конечно, шестизначное число.
Есть. Шестизначное число.
Передайте бумажку соседу, что сидит подальше от меня. А он пусть
разделит это шестизначное число на семь.
Легко сказать: разделить на семь! Может и не разделится.
Не беспокойтесь, поделится без остатка.
Числа не знаете, а уверены, что поделится.
Сначала разделите, потом будем говорить.
На ваше счастье разделилось.
Результат вручите своему соседу, не сообщая мне. Он разделит его на
11.
Думаете, опять повезет – разделится?
Делите, остатка не получится.
В самом деле без остатка! Теперь что?
Передайте результат дальше. Разделим его… ну, скажем, на 13.
Нехорошо выбрали. Без остатка на 13 мало чисел делится… Ан нет, разделилось нацело. Везет же вам!
Дайте мне бумажку с результатом; только сложите ее, чтобы я не видел числа.
Не развертывая листа бумаги, «фокусник» вручил его председателю.
Извольте получить задуманное вами число. Правильно?
Совершенно верно! – с удивлением ответил тот, взглянув на бумажку. – Именно это я и задумал… теперь, так как список ораторов исчерпан, позвольте закрыть наше собрание, благо и дождь успел пройти. Разгадки всех головоломок будут оглашены сегодня же, после ужина. Записки с решениями можете подавать мне.
Решения головоломок 1-12
Головоломка с белкой на поляне рассмотрена была полностью раньше. Переходим к следующей.
Нельзя считать, как многие делают, что 8 копеек уплачено за 8 полен, по 1 копейке за полено. Деньги эти уплачены только за третью часть от 8 полен, потому что огнем пользовались трое в одинаковой мере. Отсюда следует, что все 8 полен оценены были в 8 х 3, т. е. в 24 к., и цена одного
полена – 3 копейки.
Теперь легко сообразить, сколько причитается каждому. Пятеркиной за ее 5 полен следует 15 копеек; но она сама воспользовалась плитой на 8 копеек; значит, ей остается дополучить еще 15 – 8, т. е. 7 копеек. Тройкина за три свои полена должна получить 9 копеек, а если вычесть 8 копеек, причитающихся с нее за пользование плитой, то следовать ей будет всего только 9–8, т. е. 1 копейка.
Итак, при правильном дележе Пятеркина должна получить 7 копеек, Тройкина – 1 копейку.
содержание ..
17
18
19
20 ..
Как велик миллион?
![]()
Миллион секунд
![]()
В миллион раз толще волоса
Упражнения с миллионом
Миллиард
От великанов к карликам
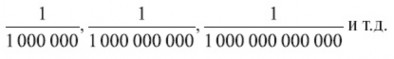

Лилипуты времени
![]()
Лилипуты пространства
Сверхисполин и сверхлилипут

![]()




![]()
Из книги «Живая математика. Математические рассказы и головоломки»
Завтрак с головоломками