содержание .. 15 16 17 18 ..
Большая книга занимательных наук (Яков Перельман) - часть 17
«Я старался, насколько мог и умел, отделаться от трудности и скуки вычислений, докучность которых обычно отпугивает весьма многих от изучения математики».
В самом деле, логарифмы чрезвычайно облегчают и ускоряют
вычисления, не говоря уже о том, что они дают возможность производить такие операции, выполнение которых без их помощи очень затруднительно (извлечение корня любой степени).
Не без основания писал Лаплас, что «изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов». Великий математик говорит об астрономах,
так как им приходится делать особенно сложные и утомительные вычисления. Но слова его с полным правом могут быть отнесены ко всем вообще, кому приходится иметь дело с числовыми выкладками.
Нам, привыкшим к употреблению логарифмов и к доставляемым ими облегчениям выкладок, трудно представить себе то изумление и восхищение, которое вызвали они при своем появлении. Современник
Непера, Бригг, прославившийся позднее изобретением десятичных логарифмов, писал, получив сочинение Непера: «Своими новыми и
удивительными логарифмами Непер заставил меня усиленно работать и головой и руками. Я надеюсь увидеть его летом, так как никогда не читал книги, которая нравилась бы мне больше и приводила бы в большее изумление». Бригг осуществил свое намерение и направился в Шотландию, чтобы посетить изобретателя логарифмов. При встрече Бригг сказал:
«Я предпринял это долгое путешествие с единственной целью видеть вас и узнать, помощью какого орудия остроумия и искусства были вы приведены к первой мысли о превосходном пособии для астрономии – логарифмах. Впрочем, теперь я больше удивляюсь тому, что никто не нашел их раньше, – настолько кажутся они простыми после того, как о них
узнаешь».
Самый поразительный из номеров, выполняемых перед публикой профессиональными счетчиками, без сомнения, следующий. Предуведомленные афишей, что счетчик-виртуоз будет извлекать в уме
корни высоких степеней из многозначных чисел, вы заготовляете дома путем терпеливых выкладок 31-ю степень какого-нибудь числа и намерены сразить счетчика 35-значным числовым линкором. В надлежащий момент вы обращаетесь к счетчику со словами:
– А попробуйте извлечь корень 31-й степени из следующего 35- значного числа! Запишите, я продиктую.
Виртуоз-вычислитель берет мел, но прежде чем вы успели открыть
рот, чтобы произнести первую цифру, у него уже написан результат: 13.
Не зная числа, он извлек из него корень, да еще 31-й степени, да еще в уме, да еще с молниеносной быстротой!..
Вы изумлены, уничтожены, а между тем во всем этом нет ничего сверхъестественного. Секрет просто в том, что существует только одно число, именно 13, которое в 31-й степени дает 35-значный результат. Числа,
меньшие 13, дают меньше 35 цифр, большие – больше.
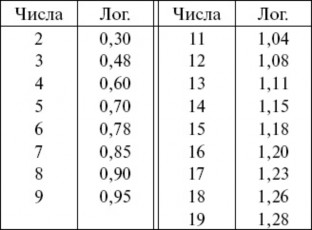
Откуда, однако, счетчик знал это? Как разыскал он число 13? Ему помогли логарифмы, двузначные логарифмы, которые он помнит наизусть
для первых 15–20 чисел. Затвердить их вовсе не так трудно, как кажется, особенно если пользоваться тем, что логарифм составного числа равен сумме логарифмов его простых множителей. Зная твердо логарифмы 2, 3 и
7 (напомним, что
, вы уже знаете логарифмы чисел первого десятка; для второго десятка требуется помнить логарифмы еще четырех чисел.
Как бы то ни было, эстрадный вычислитель мысленно располагает следующей табличкой двузначных логарифмов.
Изумивший вас математический трюк состоял в следующем:
Искомый логарифм может заключаться между
В этом интервале имеется логарифм только одного целого числа, именно 1,11 – логарифм 13. Таким путем и найден ошеломивший вас результат. Конечно, чтобы быстро проделать все это в уме, надо обладать находчивостью и сноровкой профессионала, но, по существу, дело, как видите, достаточно просто. Вы и сами можете теперь проделывать подобные фокусы, если не в уме, то на бумаге.
Пусть вам предложена задача: извлечь корень 64-й степени из 20- значного числа.
Не осведомившись о том, что это за число, вы можете объявить результат извлечения: корень равен 2.
В самом деле
; он должен, следовательно, заключаться между
и
, т. е. между 0,29 и 0,32. Такой логарифм для целого числа только один: 0,30…, т. е. логарифм числа 2.
Вы даже можете окончательно поразить загадчика, сообщив ему, какое число он собирался вам продиктовать: знаменитое «шахматное» число
264= 18 446 744 073 709 551 616.
Позволю себе начать с задачи, которую я придумал лет пятнадцать тому назад для читателей одного распространенного тогда журнала в качестве «задачи на премию». Вот она:
В бумагах одного чудака-математика найдена была его автобиография.
Она начиналась следующими строками:
«Я окончил курс университета 44-х лет от роду. Спустя год, 100- летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте – всего 11 лет – способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 10 детей. Жалованья я получал в месяц
всего 200 рублей, из которых 000/10 приходилось отдавать сестре, так что мы с детьми жили на 130 руб. в месяц» и т. д.
Чем объяснить странные противоречия в числах этого отрывка?
Решение задачи подсказывается названием этой главы: недесятичная система счисления – вот единственная причина кажущейся противоречивости приведенных чисел. Напав на эту мысль, нетрудно догадаться, в какой именно системе счисления изображены числа чудаком-
математиком. Секрет выдается фразой: «спустя год (после 44 лет), 100- летним молодым человеком…» Если от прибавления одной единицы число 44 преображается в 100, то, значит, цифра 4 – наибольшая в этой системе
(как 9 – в десятичной), а, следовательно, основанием системы является 5. Чудаку-математику пришла фантазия написать все числа своей биографии по пятиричной системе счисления, т. е. по такой, в которой единица
высшего разряда не в 10, а в 5 раз больше единицы низшего; на первом справа месте стоят в ней простые единицы (не свыше четырех), на втором – не десятки, а пятерки; на третьем не сотни, а «двадцати-пятерки», и т. д.
Поэтому число, изображенное в тексте записки «44», означает не 4 х 10 + 4, как в десятичной системе, а 4 х 5 + 4, т. е. 24.
Точно так же число «100» в автобиографии означает одну единицу
третьего разряда в пятиричной системе, т. е. 25. Остальные числа записки
соответственно означают:
Восстановив истинный смысл чисел записки, мы видим, что в ней никаких противоречий нет:
«Я окончил курс 24 лет от роду. Спустя год, 25-летним молодым человеком, я женился на 19-летней девушке. Незначительная разница в возрасте – всего 6 лет – способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет, у меня была уже и маленькая семья из 5 детей. Жалованья я получал 50 рублей, из которых 000/5 приходилось отдавать сестре, так что мы с детьми жили на 40 руб. в месяц».
Трудно ли изображать числа в других системах счисления? Нисколько.
Положим, вы желаете число 119 изобразить в пятиричной системе. Делите 119 на 5, чтобы узнать, сколько в нем единиц первого разряда:
119: 5 = 23, остаток 4.
Значит, число простых единиц будет 4. Далее, 23 пятерки не могут стоять все во втором разряде, так как высшая цифра в пятиричной системе
– 4, и больше 4 единиц ни в одном разряде быть не должно. Делим поэтому
23 на 5:
23: 5 = 4, остаток 3.
Это показывает, что во втором разряде («пятерок») будет цифра 3, а в третьем («двадцатипятерок») – 4. Итак, 119 = 4x25 + 3x5 + 4, или в пятиричной системе – «434».
Нетрудно сообразить, что в каждой системе высшая цифра, какая может понадобиться, равна основанию этой системы без единицы.
Например, в десятичной системе высшая цифра 9, в шестиричной – 5, в
троичной – 2, в пятнадцатиричной – 14, и т. д.
Самая простая система счисления, конечно, та, для которой требуется
всего меньше цифр. В десятичной системе нужны 10 цифр (считая и 0), в пятиричной – всего 5 цифр, в троичной – 3 цифры (1, 2 и 0), в двоичной – только 2 цифры (1 и 0).
Существует ли и «единичная» система? Конечно: это система, в которой единицы высшего разряда в один раз больше единицы низшего, т. е. равны ей; другими словами, «единичной» можно назвать такую систему, в которой единицы всех разрядов имеют одинаковое значение. Это самая примитивная «система»; ею пользовался первобытный человек, делая на дереве зарубки по числу сосчитываемых предметов. Но между нею и всеми другими системами счета есть громадная разница: она лишена
главного преимущества нашей нумерации – так называемого поместного значения цифр. Действительно: в «единичной» системе знак, стоящий на третьем или на пятом месте, имеет то же значение, что и стоящий на первом месте. Между тем даже в двоичной системе единица на третьем месте (справа) уже в 4 раза (2 х 2) больше, чем на первом, а на пятом – в 16 раз больше (2 х 2 х 2 х 2). Для изображения какого-нибудь числа по
«единичной» системе нужно ровно столько же знаков, сколько было сосчитано предметов: чтобы записать сто предметов, нужно сто знаков, в двоичной же – только семь («1100100»), а в пятиричной – всего три («400»).
Вот почему «единичную» систему едва ли можно назвать «системой», по крайней мере, ее нельзя поставить рядом с остальными, так как она
принципиально от них отличается, не давая никакой экономии в изображении чисел. Если же ее откинуть, то простейшей системой счисления нужно признать систему двоичную, в которой употребляются всего две цифры:
1 и 0. При помощи единицы и нуля можно изобразить все бесконечное множество чисел. На практике система эта мало удобна – получаются слишком длинные числа; но теоретически она имеет все права считаться простейшей…
В мире чисел, как и в мире живых существ, встречаются подлинные
диковинки, редкие экземпляры, обладающие исключительными свойствами. Из таких необыкновенных чисел можно было бы составить своего рода музей числовых редкостей, настоящую «арифметическую
кунсткамеру». В ее витринах нашли бы себе место не только числовые
исполины, но и числа скромных размеров, зато выделяющиеся из ряда других какими-либо необычайными свойствами. Некоторые из них уже по внешности привлекают к себе интерес и внимание; другие открывают свои диковинные особенности лишь при более близком знакомстве.
Представленные в нашей «галерее» любопытные особенности некоторых чисел не имеют ничего общего с теми воображаемыми диковинками, которые усматривают в иных числах любители таинственного. Образчиком подобных числовых суеверий может служить следующее арифметическое соображение, неосторожно высказанное знаменитым французским писателем Виктором Гюго:
«Три – число совершенное. Единица для числа 3 то же, что диаметр для круга. Среди прочих чисел 3 то же, что круг среди фигур. Число 3 – единственное, имеющее центр. Остальные числа – эллипсы, имеющие два фокуса. Отсюда следующая особенность, присущая единственно числу 3: сложите цифры любого числа, кратного 3, сумма всегда делится без остатка на 3».
В этом туманном и мнимо глубокомысленном откровении все неверно: что ни фраза, то либо вздор, либо вовсе бессмыслица. Верно только замечание о свойстве суммы цифр, но свойство это не вытекает из сказанного и к тому же не представляет исключительной особенности числа 3: им отличается в десятичной системе также и число 9, а во всех вообще системах – числа, на единицу меньшие основания.
Диковинки нашей галереи – иного рода: в них нет ничего таинственного или неразгаданного.
Приглашаю читателя пройтись со мною по галерее таких числовых диковинок и познакомиться с некоторыми из них.
Пройдем, не останавливаясь, мимо первых витрин, заключающих числа, свойства которых нам уже знакомы. Мы знаем уже, почему попало в арифметическую кунсткамеру число 2: не потому, что оно первое четное число (первым четным числом можно, впрочем, считать не 2, а 0), а потому, что оно – основание самой удобной системы счисления.
Не удивимся мы, встретив здесь 5 – одно из наших любимейших чисел, играющее важную роль при всяких «округлениях». Не будет неожиданностью для нас найти здесь и число 9, – конечно, не как символ постоянства[65], а как число, облегчающее нам поверку арифметических действий. Но вот витрина, за стеклом которой мы видим
Чем оно замечательно? Это число месяцев в году и число единиц в дюжине. Но что, в сущности, особенного в дюжине? Не многим известно, что 12 – старинный и едва не победивший соперник числа 10 за почетный пост основания системы счисления. Культурнейший народ древнего Востока – вавилоняне и их предшественники, населявшие Двуречье, вели счет в двенадцатиричной системе счисления. И если бы не пересилившее влияние Индии, подарившей нам десятичную систему, мы, вероятно, унаследовали бы от Вавилона двенадцатиричную систему. Кое в чем мы и до сих пор платим дань этой системе, несмотря на победу десятичной. Наше пристрастие к дюжинам и гроссам[66], наше деление суток на 2 дюжины часов, деление часа на 5 дюжин минут, деление минуты на столько же секунд, наконец, деление фута на 12 дюймов (фут равен
30,479 см) – не свидетельствует разве все это (и многое другое) о том, как велико в наши дни влияние этой древней системы.
Хорошо ли, что в борьбе между дюжиной и десяткой победила последняя? Конечно, сильными союзницами десятки были и остаются наши собственные руки с десятью пальцами – живые счетные машины. Но если бы не это, то следовало бы безусловно отдать предпочтение 12 перед
Гораздо удобнее производить расчеты по двенадцатиричной системе, нежели по десятичной. Причина та, что число 10 делится без остатка только на 2 и на 5, между тем как 12 делится и на 2, и на 3, и на 4, и на 6. У 10 всего два делителя, у 12 – четыре. Преимущества двенадцатиричной системы станут вам яснее, если вы примете в соображение, что в 12-ричной системе число, оканчивающееся нулем, кратно и 2, и 3, и 4, и 6: подумайте,
как удобно дробить число, когда и 000/2, и 1/3, и 1/4 и 1/6 его должны быть целыми числами. Если же выраженное в двенадцатиричной системе число оканчивается двумя нулями, то оно должно делиться без остатка на 144, а
следовательно, и на все множители 144, т. е. на следующий длинный ряд чисел:
2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144.
Четырнадцать делителей – вместо тех восьми, которые имеют числа, написанные в 10-тичной системе, если оканчиваются двумя нулями (2, 4, 5, 10, 20, 25, 50 и 100). В нашей системе только дроби вида 000/2, 1/4, 1/5, 1/20 и
т. д. превращаются в конечные десятичные; в двенадцатиричной же
системе можно написать без знаменателя гораздо более разнообразные
дроби, и прежде всего дроби: 000/2, 1/3, 1/4, 1/6, 1/8, 1/9, 1/12, 1/36, 1/18, 1/24,
000/36, 1/48, 1/72, 1/344, которые соответственно изобразятся так:
0,6; 0,4; 0,3; 0,2; 0,16; 0,14; 0,1; 0,09; 0,08; 0,06; 0,04; 0,03; 0,02; 0,01.
Было бы, однако, большим заблуждением думать, что делимость числа может зависеть от того, в какой системе счисления оно изображено. Если орехи, заключающиеся в данном мешке, могут быть разложены в пять одинаковых куч, то это свойство их, конечно, не изменится от того, будет ли число орехов в мешке выражено числом в той или иной системе счисления, или отложено на счетах, или написано прописью, или, наконец, изображено каким-либо иным способом. Если число, написанное в двенадцатиричной системе, делится на 6 или на 72, то, будучи выражено в
другой системе счисления, например в десятичной, оно должно иметь те же делители. Разница лишь в том, что в двенадцатиричной системе делимость на 6 или на 72 легче обнаружить (число оканчивается одним или двумя нолями). Когда говорят о преимуществе двенадцатиричной системы в смысле делимости на большее число делителей, то имеют в виду, что, благодаря склонности нашей к «круглым» числам, на практике будут чаще
встречаться числа, оканчивающиеся в двенадцатиричной системе нолями.
При таких очевидных преимуществах двенадцатиричной системы неудивительно, что среди математиков раздавались голоса за полный переход на двенадцатиричную систему. Однако мы уже чересчур тесно сжились с десятичной системой, чтобы решаться на такую реформу.
Великий французский математик Лаплас так высказался по этому
вопросу 100 лет назад: «Основание нашей системы нумерации не делится на 3 и на 4, то есть на два делителя, весьма употребительные по их простоте. Присоединение двух новых знаков (цифр) дало бы системе счисления это преимущество; но такое нововведение было бы, несомненно, отвергнуто. Мы потеряли бы выгоду, породившую нашу арифметику, – именно возможность счета по пальцам рук».
Напротив, следовало бы ради единообразия перейти также в измерении дуг от употребительных градусов и минут к новым, десятичным.
Такую реформу пытались провести во Франции, но она не привилась. Не кто иной, как упомянутый Лаплас, был горячим сторонником этой реформы. Его знаменитая книга «Изложение системы мира» последовательно проводит десятичное подразделение углов: градусом он
называет не 90-ю, а 100-ю долю прямого угла, минутой – 100-ю часть
градуса и т. д. Лаплас высказался даже за десятичное подразделение часов и минут. «Однообразие системы мер требует, чтобы день был разделен на
100 часов, час на 100 минут и минута на 100 секунд», – писал он.
Вы видите, следовательно, что дюжина имеет за собой длинную историю и что число 12 не без основания очутилось в галерее числовых диковинок. Зато его соседка – «чертова дюжина», 13, фигурирует здесь не потому, что чем-либо замечательна, а скорее именно потому, что ничем не замечательна, хотя и пользуется такой мрачной славой: разве не удивительно в самом деле, что ровно ничем не выделяющееся число могло стать столь «страшным» для суеверных людей?
Как было распространено это суеверие (зародившееся в древнем Вавилоне), видно из того, что царское правительство при устройстве электрического трамвая в Петербурге долго не решалось вводить маршрут
№ 13 и пропустило его, перейдя сразу на № 14: власти думали, что публика не станет ездить в вагонах с таким «роковым» номером. Любопытно и то, что в Петербурге было немало домов, где 13-й номер квартиры был пропущен… В гостинице также нередко отсутствовала комната № 13, заменяемая № 12а. Для борьбы с этим ничем не обоснованным числовым суеверием кое-где на Западе (например, в Англии) учреждались даже
особые «клубы числа 13»…
В следующей витрине арифметической кунсткамеры перед нами
Оно замечательно не только тем, что определяет число дней в году. Прежде всего, оно при делении на 7 дает в остатке 1; эта несущественная, казалось бы, особенность числа 365 имеет большое значение для нашего семидневного календаря.
Другая особенность числа 365 не связана с календарем: 365 = 10 х 10+ 11 х 11 + 12 х 12,
то есть 365 равно сумме квадратов трех последовательных чисел,
начиная с 10-ти:
102 + 112 + 122 = 100 + 121 + 144 = 365.
Но и это еще не все – тому же равна сумма квадратов двух следующих
чисел – 13 и 14:
132 +142 = 169 + 196 = 365.
На этом свойстве числа 365 основана задача С.А. Рачинского,
изображенная на известной картине «Трудная задача» Богданова- Вельского:
Таких чисел не много наберется в нашей галерее арифметических диковинок.
В следующей витрине выставлено наибольшее из всех трехзначных чисел: 999.
Любопытная особенность числа 999 проявляется при умножении на него всякого другого трехзначного числа. Получается шестизначное произведение: первые три цифры которого есть умножаемое число, только уменьшенное на единицу, а остальные три цифры – дополнения первых до
9. Например:
Стоит лишь взглянуть на следующую строку, чтобы понять
происхождение этой особенности:
Зная эту особенность, мы можем «мгновенного» умножать любое трехзначное число на 999:
947 х 999 = 846153
509 х 999 = 508491
981 х 999 = 980019 и т. д.
А так как
999 = 9 х 111 = 3 x 3 x 3 x 37,
то вы можете, опять-таки с молниеносной быстротой, писать целые
колонны шестизначных чисел, кратных 37; незнакомый со свойствами числа 999, конечно, сделать этого не в состоянии. Короче говоря, вы можете устраивать перед непосвященными маленькие сеансы «мгновенного
умножения и деления».
Следующим на очереди у нас 1001, прославленное число Шехеразады.
Вы, вероятно, и не подозревали, что в самом названии сборника волшебных арабских сказок заключается также своего рода чудо, которое могло бы поразить воображение сказочного султана не менее многих других чудес Востока, если бы он способен был интересоваться арифметическими диковинками.
Чем же так замечательно число 1001? С виду оно кажется весьма обыкновенным. Оно даже не принадлежит к избранному разряду так называемых «простых» чисел. Оно делится без остатка, на 7, на 11 и на 13
– на три последовательных простых числа, произведением которых оно и является. Не в том диковинка, что число 1001 = 7 x 11 x 13, – здесь нет еще
ничего волшебного. Замечательнее то, что при умножении на него трехзначного числа получается результат, состоящий из умноженного числа, только написанного дважды, например:
873 х 1001 = 873873;
207 х 1001 = 207207 и т. д.
И хотя этого и следовало ожидать, так как 873 х 1001 = 873 х 1000 +
873 = 878000 + 873, – все же, пользуясь указанным свойством числа Шехеразады, можно достичь результатов, совсем неожиданных, – по крайней мере, человеку неподготовленному.
Сейчас поясним в чем дело.
Товарищей, не посвященных в арифметические тайны, вы можете поразить следующим фокусом. Пусть кто-нибудь напишет на бумажке,
секретно от вас трехзначное число, какое хочет, и затем пусть припишет к нему еще раз то же самое число. Получится шестизначное число, состоящее из трех повторяющихся цифр. Предложите тому же товарищу или его соседу разделить секретно от вас это число на 7, при этом вы заранее предсказываете, что остатка не получится. Результат передается новому соседу, который по вашему предложению делит его на 11; и хотя вы не знаете делимого, вы все же смело утверждаете, что и оно разделится без остатка. Полученный результат вы направляете следующему соседу, которого просите разделить это число на 13 – деление снова выполняется
без остатка, о чем вы заранее предупреждаете. Результат третьего деления вы, не глядя на полученное число, вручаете первому товарищу со словами:
Вот число, которое вы задумали!
Так и есть: ты угадал.
Какова разгадка фокуса?
Этот красивый арифметический фокус, производящий на непосвященных впечатление волшебства, объясняется очень просто:
вспомните, что приписать к трехзначному числу его само – значит
умножить его на 1001, т. е. на произведение 7 х 11 х 13. Шестизначное число, которое ваш товарищ получит после того, как припишет к задуманному числу его само, должно будет поэтому делиться без остатка и на 7, и на 11, и на 13, а после деления последовательно на эти три числа (т. е. на их произведение – 1001) должно снова дать первоначальное число.
После сказанного о числе 1001 для вас уже не будет неожиданностью увидеть в витринах нашей галереи число 10101. Вы догадаетесь, какому именно свойству число это обязано такою честью. Оно, как и число 1001, дает удивительный результат при умножении, но не трехзначных, а двузначных чисел: каждое двузначное число, умноженное на 10101, дает в результате само себя, написанное трижды. Например:
73 х 10101 = 737373;
21 х 10101 = 212121.
Причина уясняется из следующей строки:
Можно ли проделывать с помощью этого числа фокусы необычайного отгадывания, как с помощью числа 1001?
Да, можно. Здесь возможно даже обставить фокус разнообразнее, если иметь в виду, что 10101 есть произведение четырех простых чисел:
10101 = 3 х 7 х 13 x 37.
Предложив товарищу задумать какое-нибудь двузначное число, вы
предлагаете второму приписать к нему то же число, а третьему – приписать то же число еще раз. Четвертого вы просите разделить получившееся
шестизначное число, например, на 7; пятый товарищ должен разделить полученное частное на 3; шестой делит то, что получилось, на 37, и, наконец, седьмой делит этот результат на 13, причем все четыре деления выполняются без остатка. Результат последнего деления вы просите
передать первому товарищу: это – задуманное им число.
При повторении фокуса вы можете внести в него некоторое
разнообразие, обращаясь каждый раз к новым делителям. А именно вместо
множителей
3 х 7 х 13 х 37 можете взять следующие группы множителей:
21 х 13 х 37; 7 х 39 х 37; 3 х 91 х 37; 7 х 13 х 111.
Число это – 10101, – пожалуй, даже удивительнее волшебного числа Шехеразады, хотя и менее его известно своими поразительными свойствами. О нем писалось, впрочем, еще двести лет тому назад в
«Арифметике» Магницкого, в главе, где приводятся примеры умножения «с некоим удивлением». С тем большим основанием должны мы включить его в наше собрание арифметических диковинок.
С этим числом вы также можете проделать фокусы вроде предыдущих, хотя, пожалуй, не столь эффектные. Дело в том, что оно представляет собой произведение только двух простых чисел:
10001 = 73 х 137.
Как воспользоваться этим для выполнения арифметических действий
«с удивлением», читатель, надеюсь, после всего сказанного выше догадается сам.
В следующей витрине мы видим новую диковинку арифметической
кунсткамеры – число, состоящее из шести единиц. Благодаря знакомству с волшебными свойствами числа 1001, мы сразу соображаем, что
111111= 111 х 1001.
Но 111 = 3 х 37, а 1001 = 7 х 11 х 13. Отсюда следует, что наш новый числовой феномен, состоящий из одних лишь единиц, представляет собою произведение пяти простых множителей. Соединяя же эти пять
множителей в две группы на всевозможные лады, мы получаем 15 пар множителей, дающих в произведении одно и то же число 111111, а именно:
3 × (7 × 11 × 13 × 37) = 3 × 37037 = 111111
7 × (3 × 11 × 13 × 37) = 7 × 15873 = 111111
11 × (3 × 7 × 13 × 37) = 11 × 10101 = 111111
13 × (3 × 7 × 11 × 37) = 13 × 8547 = 111111
37 × (3 × 7 × 11 × 13) = 37 × 3003 = 111111
(3 × 7) × (11 × 13 × 37) = 21 × 5291 = 111111
(3 × 11) × (7 × 13 × 37) = 33 × 3367 = 111111
и т. д.
Вы можете, значит, засадить кружок из 15 товарищей за работу
умножения, и хотя каждый будет перемножать другую пару чисел, все получат один и тот же оригинальный результат: 111111.
То же число, 111111, пригодно и для отгадывания задуманных чисел наподобие того, как выполняется это с помощью чисел 1001 и 10101. В данном случае нужно предлагать задумывать число однозначное, т. е. цифру, и повторять 6 раз. Делителями здесь могут служить пять простых чисел: 3,7, 11, 13, 37 и получающиеся из них составные: 21, 33, 39 и т. д. Это дает возможность до крайности разнообразить выполнение фокуса. Как надо поступать в этих случаях, предоставляю подумать читателю.
На примере числа 111111 читатель видит, как можно использовать для
арифметических фокусов число, состоящее из одних лишь единиц, если оно разлагается на множители. К счастью для любителей подобных фокусов, многие числа такого начертания составные, а не простые.
Из первых 17 чисел этого рода только два наименьшие – 1 и 11 – простые, остальные – составные. Вот как разлагаются на простые множители первые десять из составных чисел этого начертания:
Не все приведенные здесь числа удобно использовать для отгадывания; в некоторых случаях выполнение фокуса возложило бы на загадчика чересчур обременительную работу. Но числа из 3, из 4, из 5, из 6, из 8, из 9, из 12 единиц более или менее пригодны для этой цели.
В следующих витринах галереи нас поражают числовые достопримечательности совсем особого рода – некоторое подобие пирамид,
составленных из чисел. Рассмотрим поближе первую из таких пирамид.
Пирамида 1
Как объяснить эти своеобразные результаты умножения?
Чтобы постичь эту странную закономерность, возьмем для примера какой-нибудь из средних рядов нашей числовой пирамиды:
123456 х 9 + 7.
Вместо умножения на 9, можно умножить на (10 – 1), т. е. приписать 0
и вычесть умножаемое:
Достаточно взглянуть на последнее вычитание, чтобы понять, почему тут получается результат, состоящий только из одних единиц.
Мы можем уяснить себе это исходя и из других рассуждений. Чтобы число вида 12345… превратилось в число вида 11111… нужно из второй его цифры вычесть
1, из третьей – 2, из четвертой – 3, из пятой – 4 и т. д. – иначе говоря,
вычесть из него то же число вида 12345…, вдесятеро уменьшенное и предварительно лишенное последней цифры. Теперь понятно, что для получения искомого результата нужно наше число умножить на 10, прибавить к нему следующую за последней цифру и вычесть из результата
первоначальное число (а умножить на 10 и отнять множимое – значит умножить на 9).
Сходным образом объясняется образование и следующей числовой пирамиды, получающейся при умножении определенного ряда цифр на 8 и прибавлении последовательно возрастающих цифр:
Пирамида 2
Особенно интересна в этой пирамиде последняя строка, где в результате умножения на 8 и прибавления 9 происходит превращение
полного натурального ряда цифр в такой же ряд, но с обратным расположением. Объясним эту особенность.
Получение странных результатов уясняется из следующей строки:[67]
то есть 12345 х 8 + 5 = 111111 – 12346. Но вычитая из числа 111111 число 12346, составленное из ряда возрастающих цифр, мы, как легко понять, должны получить ряд убывающих цифр – 98765.
Вот наконец третья числовая пирамида, также требующая объяснения:
Пирамида 3
Эта пирамида является следствием первых двух. Связь эта
устанавливается очень легко. Из первой пирамиды мы знаем уже, что, например:
12345 x 9 + 6= 111111.
Умножив обе части на 8, имеем: (12345 х 8 х 9) + (6 х 8) = 888888.
Но из второй пирамиды известно, что 12345 х 8 + 5 = 98765, или что
12345 х 8 = 98760.
Значит: 888888 = (12345 х 8 х 9) + (6 х 8) = (98760 х 9) + 48 = (98760 х
9) + (5 х 9) + 3 = (98760 + 5) х 9 + 3 = 98765 х 9 + 3.
Вы убеждаетесь, что все эти числовые пирамиды не так уже загадочны, как кажутся с первого взгляда.
содержание ..
15
16
17
18 ..
Логарифмы на эстраде
![]()

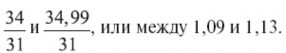
![]()
![]()
![]()
Из книги «Занимательная арифметика. Загадки и диковинки в мире чисел»
Загадочная автобиография
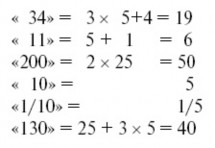
Простейшая система счисления
Арифметическая кунсткамера
![]()
Число 12
![]()
Число 365

Три девятки
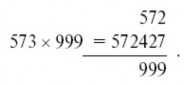

Число Шехеразады
Число 10101

Число 10001
Шесть единиц
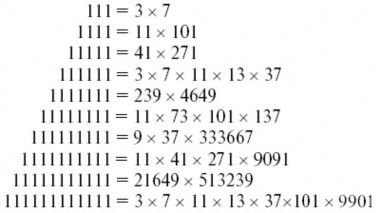
Числовые пирамиды
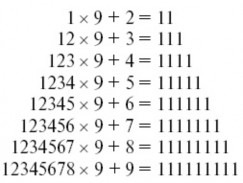
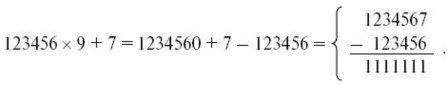

![]()

