содержание .. 13 14 15 16 ..
Большая книга занимательных наук (Яков Перельман) - часть 15
Но, может быть, Пахому еще выгоднее было бы выкроить себе участок
вовсе не прямоугольной формы, а какой-нибудь другой – четырехугольной, треугольной, пятиугольной и т. д.?
Этот вопрос может быть рассмотрен строго математически; однако из
опасения утомить нашего читателя мы не станем входить здесь в это рассмотрение и познакомим его только с результатами.
Можно доказать, во-первых, что из всех четырехугольников с
одинаковым периметром наибольшую площадь имеет квадрат. Поэтому, желая иметь четырехугольный участок, Пахом никакими ухищрениями не мог бы овладеть более чем 100 кв. верстами (считая, что максимальный
дневной пробег его – 40 верст).
Во-вторых, можно доказать, что квадрат имеет большую площадь, чем всякий треугольник равного периметра. Равносторонний треугольник
такого же периметра имеет площадь равную 77 кв. верстам, т. е. меньше
даже, чем у той трапеции, которую Пахом обошел. Из всех треугольников с равными периметрами равносторонний обладает наибольшей площадью. Значит, если даже этот наибольший треугольник имеет площадь, меньшую площади квадрата, то все прочие треугольники того же периметра по площади меньше, чем квадрат.
Но если будем сравнивать площадь квадрата с площадью пятиугольника, шестиугольника и т. д. равного периметра, то здесь первенство его прекращается: правильный пятиугольник обладает большей площадью, правильный шестиугольник – еще большей и т. д. Легко убедиться в этом на примере правильного шестиугольника.
Избери Пахом для своего участка форму правильного шестиугольника, он при том же напряжении сил овладел бы площадью на 37 кв. верст больше, чем в действительности, и на 15 кв. верст больше, чем дал бы ему квадратный участок (но для этого, конечно, пришлось бы ему пуститься в путь с угломерным инструментом).
ЗАДАЧА Из шести спичек сложить фигуру с наибольшей площадью.
РЕШЕНИЕ Из шести спичек можно составить довольно разнообразные фигуры: равносторонний треугольник, прямоугольник, множество параллелограммов, целый ряд неправильных пятиугольников, ряд неправильных шестиугольников и, наконец, правильный шестиугольник. Геометр, не сравнивая между собой площади этих фигур, заранее знает, какая фигура имеет наибольшую площадь: правильный
шестиугольник.
Можно доказать строго геометрически, что чем больше сторон у правильного многоугольного участка, тем большую площадь заключает он
при одной и той же длине границ. А самую большую площадь при данном периметре охватывает окружность. Если бы Пахом бежал по кругу, то, пробежав те же 40 верст, он получил бы площадь в 127 кв. верст.
Большей площадью при данном периметре не может обладать никакая другая фигура, безразлично – прямолинейная или криволинейная.
Легко доказать справедливость и такого положения: из всех фигур
равной площади круг имеет наименьший периметр. Для этого нужно применить к кругу те рассуждения, которые мы раньше приложили к квадрату.
ЗАДАЧА
Какой гвоздь труднее вытащить – круглый, квадратный или треугольный, – если они забиты одинаково глубоко и имеют одинаковую площадь поперечного сечения?
РЕШЕНИЕ
Будем исходить из того, что крепче держится тот гвоздь, который соприкасается с окружающим материалом по большей поверхности. У какого же из наших гвоздей большая боковая поверхность? Мы уже знаем, что при равных площадях периметр квадрата меньше периметра треугольника, а окружность меньше периметра квадрата. Если сторону квадрата принять за единицу, то вычисление дает для этих трех величин
значения: 4,53; 4; 3,55. Следовательно, крепче других должен держаться треугольный гвоздь.
Таких гвоздей, однако, не изготовляют, по крайней мере в продаже они не встречаются. Причина кроется, вероятно, в том, что подобные гвозди легче изгибаются и ломаются.
Свойством, сходным со свойством круга, обладает и шаровая поверхность: она имеет наибольший объем при данной величине поверхности. И наоборот, из всех тел одинакового объема наименьшую поверхность имеет шар.
Эти свойства не лишены значения в практической жизни. Шарообразный самовар обладает меньшей поверхностью, чем
цилиндрический или какой-либо иной формы, вмещающий столько же стаканов, а так как тело теряет теплоту только с поверхности, то шарообразный самовар остывает медленнее, чем всякий другой того же
объема. Напротив, резервуар градусника быстрее нагревается и охлаждается (т. е. принимает температуру окружающих предметов), когда ему придают форму не шарика, а цилиндра.
По той же причине земной шар, состоящий из твердой оболочки и
ядра, должен уменьшаться в объеме, т. е. сжиматься, уплотняться, от всех причин, изменяющих форму его поверхности: его внутреннему
содержимому должно становиться тесно всякий раз, когда наружная его
форма претерпевает какое-либо изменение, отклоняясь от шара. Возможно,
что этот геометрический факт находится в связи с землетрясениями и вообще с тектоническими явлениями, но об этом должны иметь суждение геологи.
Алгебру называют нередко «арифметикой семи действий», подчеркивая, что к четырем общеизвестным математическим операциям
она присоединяет три новых: возведение в степень и два ему обратных действия.
Наши алгебраические беседы начнутся с «пятого действия» – возведения в степень.
Вызвана ли потребность в этом новом действии практической жизнью? Безусловно. Мы очень часто сталкиваемся с ним в реальной
действительности. Вспомним о многочисленных случаях вычисления площадей и объемов, где обычно приходится возводить числа во вторую и третью степени. Далее: сила всемирного тяготения, электростатическое и магнитное взаимодействия, свет, звук ослабевают пропорционально второй степени расстояния. Продолжительность обращения планет вокруг Солнца (и спутников вокруг планет) связана с расстояниями от центра обращения
также степенной зависимостью: вторые степени времен обращения относятся между собою, как третьи степени расстояний.
Не надо думать, что практика сталкивает нас только со вторыми и третьими степенями, а более высокие показатели существуют только в упражнениях алгебраических задачников. Инженер, производя расчеты на прочность, сплошь и рядом имеет дело с четвертыми степенями, а при
других вычислениях (например, диаметра паропровода) – даже с шестой степенью. Исследуя силу, с какой текучая вода увлекает камни,
гидротехник наталкивается на зависимость также шестой степени: если
скорость течения в одной реке вчетверо больше, чем в другой, то быстрая река способна перекатывать по своему ложу камни в 46, т. е. в 4096 раз более тяжелые, чем медленная[58].
С еще более высокими степенями встречаемся мы, изучая зависимость яркости раскаленного тела – например, нити накала в электрической
лампочке – от температуры. Общая яркость растет при белом калении с двенадцатой степенью температуры, а при красном – с тридцатой степенью
температуры («абсолютной», т. е. считаемой от минус 273°). Это означает,
что тело, нагретое, например, от 2000° до 4000° (абсолютных), т. е. в два
раза сильнее, становится ярче в 212, иначе говоря, более чем в 4000 раз.
Никто, пожалуй, не пользуется так широко пятым математическим действием, как астрономы. Исследователям Вселенной на каждом шагу приходится встречаться с огромными числами, состоящими из одной-двух значащих цифр и длинного ряда нулей.
Изображение обычным образом подобных числовых исполинов, справедливо называемых «астрономическими числами», неизбежно вело бы к большим неудобствам, особенно при вычислениях. Расстояние, например, до туманности Андромеды, написанное обычным порядком, представляется таким числом километров:
95 000 000 000 000 000 000.
При выполнении астрономических расчетов приходится к тому же
выражать зачастую небесные расстояния не в километрах или более крупных единицах, а в сантиметрах. Рассмотренное расстояние изобразится в этом случае числом, имеющим на пять нулей больше:
9 500 000 000 000 000 000 000 000.
Массы звезд выражаются еще большими числами, особенно если их выражать, как требуется для многих расчетов, в граммах. Масса нашего
Солнца в граммах равна:
1 983 000 000 000 000 000 000 000 000 000 000.
Легко представить себе, как затруднительно было бы производить вычисления с такими громоздкими числами и как легко было бы при этом ошибиться. А ведь здесь приведены далеко еще не самые большие астрономические числа.
Пятое математическое действие дает вычислителям простой выход из этого затруднения. Единица, сопровождаемая рядом нулей, представляет собой определенную степень десяти:
100 = 102, 1000 = 103, 10 0 00 = 104 и т. д.
Приведенные раньше числовые великаны могут быть поэтому представлены в таком виде:
первый……… 950 · 1023
второй……… 1983 · 1030
Делается это не только для сбережения места, но и для облегчения
расчетов. Если бы потребовалось, например, оба эти числа перемножить, то
достаточно было бы найти произведение 95 · 1983 = 188 385 и поставить
его впереди множителя 1023+30= 1053:
950 · 1023 · 1983 · 1030 = 188 385 · 1053.
Это, конечно, гораздо удобнее, чем выписывать сначала число с 21 нулем, затем с 30 и, наконец, с 53 нулями, – не только удобнее, но и надежнее, так как при писании десятков нулей можно проглядеть один-два нуля и получить неверный результат.
Чтобы убедиться, насколько облегчаются практические вычисления при пользовании степенным изображением больших чисел, выполним такой расчет: определим, во сколько раз масса земного шара больше массы всего окружающего его воздуха.
На каждый кв. сантиметр земной поверхности воздух давит, мы знаем, с силой около килограмма. Это означает, что вес того столба атмосферы, который опирается на 1 кв. см, равен 1 кг. Атмосферная оболочка Земли как бы составлена вся из таких воздушных столбов; их столько, сколько кв. сантиметров содержит поверхность нашей планеты; столько же килограммов весит вся атмосфера. Заглянув в справочник, узнаем, что величина поверхности земного шара равна 510 млн. кв. км, т. е. 51·107 кв.
км.
Рассчитаем, сколько квадратных сантиметров в квадратном километре. Линейный километр содержит 1000 м, по 100 см в каждом, т. е. равен 105 см, а кв. километр содержит (105)2 = 1010кв. сантиметров. Во всей поверхности земного шара заключается поэтому:
51·107 -1010 = 51·1017
кв. сантиметров. Столько же килограммов весит и атмосфера Земли.
Переведя в тонны, получим:
51·1017: 1000 = 51·1017: 103 = 51·1017-3 = 51·1014.
Масса же земного шара выражается числом:
6 · 1021 тонн.
Чтобы определить, во сколько раз наша планета тяжелее ее воздушной оболочки, производим деление:
6 · 1021:51·1014 ≈ 106,
т. е. масса атмосферы составляет примерно миллионную долю массы земного шара.
Если вы спросите у химика, почему дрова или уголь горят только при
высокой температуре, он скажет вам, что соединение углерода с кислородом происходит, строго говоря, при всякой температуре, но при низких температурах процесс этот протекает чрезвычайно медленно (т. е. в реакцию вступает весьма незначительное число молекул) и потому ускользает от нашего наблюдения. Закон, определяющий скорость химических реакций, гласит, что с понижением температуры на 10° скорость реакции (число участвующих в ней молекул)
уменьшается в два раза.
Применим сказанное к реакции соединения древесины с кислородом, т. е. к процессу горения дров. Пусть при температуре пламени 600° сгорает
ежесекундно 1 грамм древесины. Во сколько времени сгорит 1 грамм дерева при 20°? Мы уже знаем, что при температуре, которая на 580 = 58– 10 градусов ниже, скорость реакции меньше в
258 раз,
т. е. 1 грамм дерева сгорит в 258 секунд.
Скольким годам равен такой промежуток времени? Мы можем
приблизительно подсчитать это, не производя 57 повторных умножений на два и обходясь без логарифмических таблиц. Воспользуемся тем, что
210= 1024 ≈ 103.
Следовательно,
т. е. около четверти триллиона секунд. В году около 30 млн., т. е. 3·107, секунд; поэтому
Десять миллиардов лет! Вот во сколько примерно времени сгорел бы грамм дерева без пламени и жара.
Итак, дерево, уголь горят и при обычной температуре, не будучи вовсе подожжены. Изобретение орудий добывания огня ускорило этот страшно
медленный процесс в миллиарды раз.
ЗАДАЧА
Будем характеризовать погоду только по одному признаку, – покрыто
ли небо облаками или нет, т. е. станем различать лишь дни ясные и
пасмурные. Как вы думаете, много ли при таком условии возможно недель с различным чередованием погоды?
Казалось бы, немного: пройдет месяца два, и все комбинации ясных и пасмурных дней в неделе будут исчерпаны; тогда неизбежно повторится одна из тех комбинаций, которые уже наблюдались прежде.
Попробуем, однако, точно подсчитать, сколько различных комбинаций возможно при таких условиях. Это – одна из задач, неожиданно приводящих к пятому математическому действию.
Итак: сколькими различными способами могут на одной неделе чередоваться ясные и пасмурные дни?
РЕШЕНИЕ
Первый день недели может быть либо ясный, либо пасмурный; имеем, значит, пока две «комбинации».
В течение двухдневного периода возможны следующие чередования ясных и пасмурных дней:
ясный и ясный ясный и пасмурный пасмурный и ясный
пасмурный и пасмурный.
Итого в течение двух дней 22 различного рода чередований. В трехдневный промежуток каждая из четырех комбинаций первых двух дней сочетается с двумя комбинациями третьего дня; всех родов чередований
будет
22 · 2 = 23.
В течение четырех дней число чередований достигнет 23 · 2 = 24.
За пять дней возможно 25, за шесть дней 26 и, наконец, за неделю 27= 128 различного рода чередований.
Отсюда следует, что недель с различным порядком следования ясных и пасмурных дней имеется 128. Спустя 128 · 7 = 896 дней непременно должно повториться одно из прежде бывших сочетаний; повторение,
конечно, может случиться и раньше, но 896 дней – срок, по истечении которого такое повторение неизбежно. И обратно: может пройти целых два года, даже больше (2 года и 166 дней), в течение которых ни одна неделя по погоде не будет похожа на другую.
ЗАДАЧА
В одном советском учреждении обнаружен был несгораемый шкаф, сохранившийся с дореволюционных лет. Отыскался и ключ к нему, но чтобы им воспользоваться, нужно было знать секрет замка; дверь шкафа открывалась лишь тогда, когда имевшиеся на двери 5 кружков с алфавитом на их ободах (36 букв) устанавливались на определенное слово. Так как никто этого слова не знал, то, чтобы не взламывать шкафа, решено было перепробовать все комбинации букв в кружках. На составление одной комбинации требовалось 3 секунды времени.
Можно ли надеяться, что шкаф будет открыт в течение ближайших 10
рабочих дней?
РЕШЕНИЕ
Подсчитаем, сколько всех буквенных комбинаций надо было перепробовать.
Каждая из 36 букв первого кружка может сопоставляться с каждой из 36 букв второго кружка. Значит, двухбуквенных комбинаций возможно
36 · 36 = 362.
К каждой из этих комбинаций можно присоединить любую из 36 букв третьего кружка. Поэтому трехбуквенных комбинаций возможно
362 · 36 = 363.
Таким же образом определяем, что четырехбуквенных комбинаций может быть 364, а пятибуквенных 365, или 60 466 176. Чтобы составить эти
60 с лишним миллионов комбинаций, потребовалось бы времени, считая по 3 секунды на каждую,
3 · 60 466 176 = 181 398 528
секунд. Это составляет более 50 000 часов, или почти 6300 восьмичасовых рабочих дней – более 20 лет.
Значит, шансов на то, что шкаф будет открыт в течение ближайших 10 рабочих дней, имеется 10 на 6300, или один из 630. Это очень малая вероятность.
Разительный пример чрезвычайно быстрого возрастания самой маленькой величины при повторном ее удвоении дает общеизвестная легенда о награде изобретателю шахматной игры[59]. Не останавливаясь на этом классическом примере, приведу другие, не столь широко известные.
ЗАДАЧА
Инфузория парамеция каждые 27 часов (в среднем) делится пополам. Если бы все нарождающиеся таким образом инфузории оставались в живых, то сколько понадобилось бы времени, чтобы потомство одной парамеции заняло объем, равный объему Солнца?
Данные для расчета: 40-е поколение парамеций, не погибающих после деления, занимает в объеме 1 куб. м; объем Солнца примем равным 1027 куб. м.
РЕШЕНИЕ
Задача сводится к тому, чтобы определить, сколько раз нужно удваивать 1 куб. м, чтобы получить объем в 1027 куб. м. Делаем преобразования:
1027 = (103)9 ≈ (210)9 = 290,
так как 210 ≈ 1000.
Значит, сороковое поколение должно претерпеть еще 90 делений,
чтобы вырасти до объема Солнца. Общее число поколений, считая от первого, равно 40 + 90 = 130. Легко сосчитать, что это произойдет на 147-е сутки.
Заметим, что фактически одним микробиологом (Метальниковым) наблюдалось 8061 деление парамеции. Предоставляю читателю самому рассчитать, какой колоссальный объем заняло бы последнее поколение,
если бы ни одна инфузория из этого количества не погибла…
Вопрос, рассмотренный в этой задаче, можно предложить, так сказать, в обратном виде.
Вообразим, что наше Солнце разделилось пополам, половина также разделилась пополам и т. д. Сколько понадобится таких делений, чтобы получились частицы величиной с инфузорию?
Хотя ответ уже известен читателям – 130, он все же поражает своею несоразмерной скромностью.
Мне предложили ту же задачу в такой форме.
Листок бумаги разрывают пополам, одну из полученных половин снова делят пополам и т. д. Сколько понадобится делений, чтобы получить частицы атомных размеров?
Допустим, что бумажный лист весит 1 г, и примем для веса атома
величину порядка
. Так как в последнем выражении можно заменить 1024 приближенно
равным ему выражением 280, то ясно, что делений пополам потребуется всего 80, а вовсе не миллионы, как приходится иногда слышать в ответ на вопрос этой задачи.
Всем, вероятно, известно, как следует написать три цифры, чтобы изобразить ими возможно большее число. Надо взять три девятки и расположить их так:
т. е. написать третью «сверхстепень» от 9.
Число это столь чудовищно велико, что никакие сравнения не помогают уяснить себе его грандиозность. Число электронов видимой
Вселенной ничтожно по сравнению с ним. В моей «Занимательной арифметике» (глава десятая) уже говорилось об этом. Возвращаюсь к этой задаче лишь потому, что хочу предложить здесь по ее образцу другую.
Тремя двойками, не употребляя знаков действий, написать возможно большее число.
РЕШЕНИЕ
Под свежим впечатлением трехъярусного расположения девяток вы,
вероятно, готовы дать и двойкам такое же расположение:
Однако на этот раз ожидаемого эффекта не получается. Написанное
число невелико – меньше даже, чем 222. В самом деле: ведь мы написали всего лишь 24, т. е. 16.
Подлинно наибольшее число из трех двоек – не 222 и не 222 (т. е. 484),
а
222 = 4 194 304.
Пример очень поучителен. Он показывает, что в математике опасно
поступать по аналогии; она легко может повести к ошибочным заключениям.
ЗАДАЧА
Теперь, вероятно, вы осмотрительнее приступите к решению следующей задачи.
Тремя тройками, не употребляя знаков действий, написать возможно большее число.
РЕШЕНИЕ
Трехъярусное расположение и здесь не приводит к ожидаемому эффекту, так как
Последнее расположение и дает ответ на вопрос задачи.
ЗАДАЧА
Тремя четверками, не употребляя знаков действий, написать возможно
большее число.
РЕШЕНИЕ
Если в данном случае вы поступите по образцу двух предыдущих задач, т. е. дадите ответ
444,
то ошибетесь, потому что на этот раз трехъярусное расположение
как раз дает большее число. В самом деле, 44 = 256, а 4256 больше, чем 444.
Попытаемся углубиться в это озадачивающее явление и установить, почему одни цифры порождают числовые исполины при трехъярусном расположении, другие – нет. Рассмотрим общий случай.
Тремя одинаковыми цифрами, не употребляя знаков действий, изобразить возможно большее число. Обозначим цифру буквой а. Расположению
222, 333, 444
соответствует написание
а 10
а +
а , т. е.
а 11
а .
Расположение же трехъярусное представится в общем виде так:
Определим, при каком значении а последнее расположение изображает большее число, нежели первое. Так как оба выражения представляют степени с равными целыми основаниями, то бо́льшая величина отвечает
большему показателю. Когда же
аа> 11а?
Разделим обе части неравенства на а. Получим:
аа-1> 11.
Легко видеть, что аа-1 больше 11 только при условии, что а больше 3, потому что
44–1 > 11,
между тем как степени З2 и 21
меньше 11.
Теперь понятны те неожиданности, с которыми мы сталкивались при решении предыдущих задач: для двоек и троек надо было брать одно
расположение, для четверок и больших чисел – другое.
ЗАДАЧА
Четырьмя единицами, не употребляя никаких знаков математических действий, написать возможно большее число.
РЕШЕНИЕ
Естественно приходящее на ум число – 1111 – не отвечает требованию
задачи, так как степень
1111
во много раз больше. Вычислять это число десятикратным умножением на 11 едва ли у кого хватит терпения. Но можно оценить его величину гораздо быстрее с помощью логарифмических таблиц.
Число это превышает 285 миллиардов и, следовательно, больше числа 1111 в 25 с лишним млн. раз.
ЗАДАЧА
Сделаем следующий шаг в развитии задач рассматриваемого рода и поставим наш вопрос для четырех двоек.
При каком расположении четыре двойки изображают наибольшее число?
РЕШЕНИЕ
Возможны 8 комбинаций:
Какое же из этих чисел наибольшее?
Займемся сначала верхним рядом, т. е. числами в двухъярусном расположении.
Первое – 2222, – очевидно меньше трех прочих. Чтобы сравнить следующие два —
2222 и 2222,
преобразуем второе из них: 2222 = 22211 = (222)11 = 48411.
Последнее число больше, нежели 2222, так как и основание, и показатель у степени 48411 больше, чем у степени 2222.
Сравним теперь 2222 с четвертым числом первой строки – с 2222. Заменим 2222 большим числом 3222 и покажем, что даже это большее
число уступает по величине числу 2222. В самом деле,
3222=(25)22= 2110
– степень меньшая, нежели 2222.
Итак, наибольшее число верхней строки – 2222. Теперь нам остается сравнить между собой пять чисел – сейчас полученное и следующие четыре:
Последнее число, равное всего 216, сразу выбывает из состязания. Далее, первое число этого ряда, равное 224 и меньшее, чем 324 или 220,
меньше каждого из двух следующих. Подлежат сравнению, следовательно, три числа, каждое из которых есть степень 2. Больше, очевидно, та степень 2, показатель которой больше. Но из трех показателей
222,484 и 220+2 (=210·2·22 ≈ 106·4)
содержание ..
13
14
15
16 ..
Участки другой формы
Фигуры с наибольшей площадью
Гвозди
Тело наибольшего объема
Из книги «Занимательная алгебра»
Пятое действие
![]()
Астрономические числа
Сколько весит весь воздух
Горение без пламени и жара
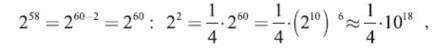
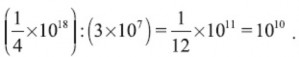
Разнообразие погоды
Замо́к с секретом
Итоги повторного удвоения
![]()
![]()
Тремя двойками
![]()
![]()
Тремя тройками
![]()
Тремя четверками
![]()
Тремя одинаковыми цифрами
![]()
Четырьмя единицами
Четырьмя двойками

![]()