содержание .. 11 12 13 14 ..
Большая книга занимательных наук (Яков Перельман) - часть 13
Для измерения углов на местности нам нужен хотя бы компас, а иной раз достаточно и собственных пальцев или спичечной коробки. Но может возникнуть необходимость измерить угол, нанесенный на бумагу, на план или на карту.
Разумеется, если есть под руками транспортир, то вопрос решается просто. А если транспортира нет, например в походных условиях? Геометр не должен растеряться и в этом случае. Как бы вы решили следующую
задачу?
ЗАДАЧА Изображен угол АОВ (рис. 6), меньший 180°. Определить его величину без измерений.
РЕШЕНИЕ
Можно было бы из произвольной точки стороны ВО опустить перпендикуляр на сторону АО, в получившемся прямоугольном треугольнике измерить катеты и гипотенузу, найти синус угла, а затем и
величину самого угла. Но такое решение задачи не соответствовало бы жесткому условию – ничего не измерять!
Рис. 6. Как определить величину изображенного угла ЛОВ, пользуясь только циркулем?
Воспользуемся решением, предложенным в 1946 г. 3. Рупейка из Каунаса.
Из вершины О, как из центра, произвольным раствором циркуля построим полную окружность. Точки С и D ее пересечения со сторонами угла соединим отрезком прямой.
Теперь от начальной точки С на окружности будем откладывать последовательно при помощи циркуля хорду CD в одном и том же
направлении до тех пор, пока ножка циркуля опять совпадет с исходной точкой С.
Откладывая хорды, мы должны считать, сколько раз за это время будет обойдена окружность и сколько раз будет отложена хорда.
Допустим, что окружность мы обошли п раз и за это время S раз отложили хорду CD. Тогда искомый угол будет равен
Действительно, пусть данный угол содержит х°; отложив на окружности хорду CD S раз, мы как бы увеличили угол х° в S раз, но так как окружность при этом оказалась пройденной п раз, то этот угол составит 360° · п, т. е. х°– S = 360° · п; отсюда
Для угла, изображенного на чертеже, п = 3, S = 20 (проверьте!), следовательно,
. При отсутствии циркуля окружность можно описать при помощи булавки и полоски бумаги; хорду можно откладывать при помощи той же
бумажной полоски.
Интересно отметить одно загадочное явление, которое наблюдается у
людей, бродящих с закрытыми глазами: они не могут идти по прямому
направлению, а непременно сбиваются в сторону, описывая дугу,
воображая, однако, что движутся прямо вперед (рис. 7).
Давно замечено также, что и путешественники, странствующие без компаса по пустыне, по степи в метель или в туманную погоду, – вообще во всех случаях, когда нет возможности ориентироваться, – сбиваются с прямого пути и блуждают по кругу, по нескольку раз возвращаясь к одному и тому же месту. Радиус круга, описываемого при этом пешеходом, – около 60—100 м; чем быстрее ходьба, тем радиус круга меньше, т. е. тем теснее замыкаемые круги.
Производились даже специальные опыты для изучения склонности людей сбиваться с прямого пути на круговой. Вот что сообщает о таких опытах Герой Советского Союза И. Спирин:
«На гладком зеленом аэродроме были выстроены сто будущих летчиков. Всем им завязали глаза и предложили идти прямо вперед. Люди пошли… Сперва они шли прямо; потом одни стали забирать вправо, другие
– влево, постепенно начали делать круги, возвращаясь к своим старым следам».
Рис. 7. Ходьба с закрытыми глазами
Известен аналогичный опыт в Венеции на площади Марка. Людям
завязывали глаза, ставили их на одном конце площади, как раз против собора, и предлагали до него дойти. Хотя пройти надо было всего только 175 м, все же ни один из испытуемых не дошел до фасада здания (82 м ширины), а все уклонялись в сторону, описывали дугу и упирались в одну из боковых колоннад (рис. 8).
Рис. 8. Схема опыта на площади Марка в Венеции
Кто читал роман Жюля Верна «Приключения капитана Гаттераса», тот помнит, вероятно, эпизод о том, как путешественники наткнулись в снежной необитаемой пустыне на чьи-то следы:
«– Это наши следы, друзья мои! – воскликнул доктор. – Мы заблудились в тумане и набрели на свои же собственные следы…».
Классическое описание подобного блуждания по кругу оставил нам Л.H. Толстой в рассказе «Хозяин и работник»:
«Василий Андреич гнал лошадь туда, где он почему-то предполагал лес и сторожку. Снег слепил ему глаза, а ветер, казалось, хотел остановить его, но он, нагнувшись вперед, не переставая гнал лошадь.
Минут пять он ехал, как ему казалось, все прямо, ничего не видя, кроме головы лошади и белой пустыни.
Вдруг перед ним зачернело что-то. Сердце радостно забилось в нем, и
он поехал на это черное, уже видя в нем стены домов деревни. Но черное это было выросший на меже высокий чернобыльник… И почему-то вид этого чернобыльника, мучимого немилосердным ветром, заставил
содрогнуться Василия Андреича, и он поспешно стал погонять лошадь, не замечая того, что, подъезжая к чернобыльнику, он совершенно изменил прежнее направление.
Опять впереди его зачернело что-то. Это была опять межа, поросшая
чернобыльником. Опять так же отчаянно трепался сухой бурьян. Подле него шел конный, заносимый ветром след. Василий Андреич остановился, нагнулся, пригляделся: это был лошадиный, слегка занесенный след и не мог быть ничей иной, как его собственный. Он, очевидно, кружился и на небольшом пространстве».
Норвежский физиолог Гульдберг, посвятивший кружению специальное исследование (1896 г.), собрал ряд тщательно проверенных свидетельств о подлинных случаях подобного рода. Приведем два примера.
Рис. 9. Схема блуждания трех путников
Трое путников намеревались в снежную ночь покинуть сторожку и выбраться из долины шириной в 4 км, чтобы достичь своего дома,
расположенного в направлении, которое на прилагаемом рисунке отмечено пунктиром (рис. 9). В пути они незаметно уклонились вправо, по кривой, отмеченной стрелкой. Пройдя некоторое расстояние, они, по расчету
времени, полагали, что достигли цели, – на самом же деле очутились у той же сторожки, которую покинули. Отправившись в путь вторично, они уклонились еще сильнее и снова дошли до исходного пункта. То же
повторилось в третий и четвертый раз. В отчаянии предприняли они пятую попытку, – но с тем же результатом. После пятого круга они отказались от дальнейших попыток выбраться из долины и дождались утра.
Еще труднее грести на море по прямой линии в темную беззвездную
ночь или в густой туман. Отмечен случай, – один из многих подобных, – когда гребцы, решив переплыть в туманную погоду пролив шириной в
4 км, дважды побывали у противоположного берега, но не достигли его, а бессознательно описали два круга и высадились, наконец… в месте своего отправления (рис. 10).
Рис. 10. Как гребцы пытались переплыть пролив в туманную погоду
То же случается и с животными. Полярные путешественники рассказывают о кругах, которые описывают в снежных пустынях
животные, запряженные в сани. Собаки, которых пускают плавать с завязанными глазами, также описывают в воде круги. По кругу же летят и ослепленные птицы. Затравленный зверь, лишившийся от страха способности ориентироваться, спасается не по прямой линии, а по спирали.
Зоологи установили, что головастики, крабы, медузы, даже микроскопические амебы в капле воды – все движутся по кругу.
Чем же объясняется загадочная приверженность человека и животных к кругу, невозможность держаться в темноте прямого направления?
Вопрос сразу утратит в наших глазах окутывающую его мнимую
таинственность, если мы его правильно поставим.
Спросим не о том, почему животные движутся по кругу, а о том, что им необходимо для движения по прямой линии?
Вспомните, как движется игрушечная заводная тележка. Бывает и так,
что тележка катится не по прямой, а сворачивает в сторону.
В этом движении по дуге никто не увидит ничего загадочного; каждый догадается, отчего это происходит: очевидно, правые колеса не равны левым.
Понятно, что и живое существо в том лишь случае может без помощи глаз двигаться в точности по прямой лилии, если мускулы его правой и левой сторон работают совершенно одинаково. Но в том-то и дело, что симметрия тела человека и животных неполная. У огромного большинства людей и животных мускулы правой стороны тела развиты неодинаково с мускулами левой. Естественно, что пешеход, все время выносящий правую ногу немного дальше, чем левую, не сможет держаться прямой линии; если
глаза не помогут ему выправлять его путь, он неизбежно будет забирать влево. Точно так же и гребец, когда он из-за тумана лишен возможности ориентироваться, неизбежно будет забирать влево, если его правая рука работает сильнее левой. Это – геометрическая необходимость.
Представьте себе, например, что, занося левую ногу, человек делает шаг на миллиметр длиннее, чем правой ногой. Тогда, сделав попеременно
каждой ногой тысячу шагов, человек опишет левой ногой путь на 1 000 мм, т. е. на целый метр, длиннее, чем правой. На прямых параллельных путях это невозможно, зато вполне осуществимо на концентрических окружностях…
По сходной причине лодочник, гребущий правой рукой сильнее, чем левой, должен неизбежно увлекать лодку по кругу, загибая в левую сторону.
Животные, делающие неодинаковые шаги правыми или левыми ногами, или птицы, делающие неравной силы взмахи правым и левым крылом, также должны двигаться по кругам всякий раз, когда лишены возможности контролировать прямолинейное направление зрением. Здесь тоже достаточно весьма незначительной разницы в силе рук, ног или крыльев.
При таком взгляде на дело указанные раньше факты утрачивают свою таинственность и становятся вполне естественными. Удивительно было бы, если бы люди и животные, наоборот, могли выдерживать прямое направление, не контролируя его глазами. Ведь необходимым условием для
этого является строго геометрическая симметрия тела, абсолютно невозможная для произведения живой природы. Малейшее же уклонение от математически совершенной симметрии должно повлечь за собой, как неизбежное следствие, движение по дуге. Чудо не то, чему мы здесь
удивляемся, а то, что мы готовы были считать естественным.
Невозможность держаться прямого пути не составляет для человека существенной помехи: компас, дороги, карты спасают его в большинстве
случаев от последствий этого недостатка.
Не то у животных, особенно у обитателей пустынь, степей, безграничного морского простора: для них несимметричность тела, заставляющая их описывать круги вместо прямых линий, – важный жизненный фактор. Словно невидимой цепью приковывает он их к месту рождения, лишая возможности удаляться от него сколько-нибудь значительно. Лев, отважившийся уйти подальше в пустыню, неизбежно возвращается обратно. Чайки, покидающие родные скалы для полета в открытое море, не могут не возвращаться к гнезду (тем загадочнее, однако, далекие перелеты птиц, пересекающих по прямому направлению материки и океаны).
Майн-ридовский мальчик мог успешно разрешить свою геометрическую задачу только потому, что незадолго до путешествия измерил свой рост и твердо помнил результаты измерения. Хорошо бы каждому из нас обзавестись таким «живым метром», чтобы в случае нужды
пользоваться им для измерения. Полезно также помнить, что у большинства людей расстояние между концами расставленных рук равно росту (рис. 11) – правило, подмеченное гениальным художником и ученым Леонардо да Винчи: оно позволяет пользоваться нашими «живыми метрами» удобнее, чем делал это мальчик у Майн Рида. В среднем высота взрослого человека (славянской расы) около 1,7 м, или 170 см; это легко запомнить. Но полагаться на среднюю величину не следует; каждый
должен измерить свой рост и размах своих рук.
Рис. 11. Правило Леонардо да Винчи
Для отмеривания – без масштаба – мелких расстояний следует помнить длину своей «четверти», т. е. расстояние между концами
расставленных большого пальца и мизинца (рис. 12). У взрослого мужчины оно составляет около 18 см – примерно 000/4 аршина (откуда и название
«четверть»), но у людей молодых оно меньше и медленно увеличивается с возрастом (до 25 лет).
Рис. 12. Измерение расстояния между концами пальцев
Рис. 13. Измерение длины указательного пальца
Далее, для этой же цели полезно измерить и запомнить длину своего указательного пальца, считая ее двояко: от основания среднего пальца (рис. 13) и от основания большого. Точно так же должно быть известно вам наибольшее расстояние между концами указательного и среднего пальцев, – у взрослого около 10 см (рис. 14). Надо, наконец, знать и ширину своих пальцев. Ширина трех средних пальцев, плотно сжатых, примерно 5 см.
Рис. 14. Измерение расстояния между концами двух пальцев Вооруженные всеми этими сведениями, вы сможете довольно
удовлетворительно выполнять разнообразные измерения буквально голыми
руками, даже и в темноте. Пример представлен на рис. 15: здесь измеряется пальцами окружность стакана. Исходя из средних величин, можно сказать, что длина окружности стакана приблизительно равна 23 см.
Рис. 15. Измерение окружности стакана «голыми руками»
Любой школьник вычисляет теперь длину окружности по диаметру гораздо точнее, чем мудрейший жрец древней страны пирамид или самый искусный архитектор великого Рима. Древние египтяне считали, что окружность длиннее диаметра в 3,16 раза, а римляне – в 3,12, между тем правильное отношение – 3,14159… Египетские и римские математики
установили отношение длины окружности к диаметру не строгим геометрическим расчетом, как позднейшие математики, а нашли его просто из опыта. Но почему получались у них такие ошибки? Разве не могли они
обтянуть какую-нибудь круглую вещь ниткой и затем, выпрямив нитку, просто измерить ее?
Без сомнения, они так и поступали; но не следует думать, что
подобный способ должен непременно дать хороший результат. Вообразите, например, вазу с круглым дном диаметром в 100 мм. Длина окружности дна должна равняться 314 мм. Однако на практике, измеряя ниткой, вы едва
ли получите эту длину: легко ошибиться на один миллиметр, и тогда к окажется равным 3,13 или 3,15. А если примете во внимание, что и диаметр вазы нельзя измерить вполне точно, что и здесь ошибка в 1 мм весьма
вероятна, то убедитесь, что для
п получаются довольно широкие пределы
между
т. е. в десятичных дробях между 3,09 и 3,18.
Вы видите, что, определяя я указанным способом, мы можем получить результат, не совпадающий с 3,14: один раз получим 3,1, другой раз 3,12, третий 3,17 и т. п. Случайно может оказаться среди них и 3,14, но в глазах вычислителя это число не будет иметь больше веса, чем другие.
Такого рода опытный путь никак не может дать сколько-нибудь приемлемого значения для к. В связи с этим становится более понятным, почему Древний мир не знал правильного отношения длины окружности к диаметру, и понадобился гений Архимеда, чтобы найти для я значение 3000/7
– найти без измерений, одними лишь рассуждениями.
В «Алгебре» древнего арабского математика Магомета-бен-Муза о вычислении длины окружности читаем такие строки:
«Лучший способ – это умножить диаметр на 3000/7. Это самый скорый и
самый легкий способ. Богу известно лучшее».
Теперь мы знаем, что и архимедово число 3000/7 не вполне точно выражает отношение длины окружности к диаметру Теоретически доказано, что отношение это вообще не может быть выражено какой-либо точной дробью. Мы можем написать его лишь с тем или иным приближением, впрочем, далеко превосходящим точность, необходимую
для самых строгих требований практической жизни. Математик XVI века Лудольф в Лейдене имел терпение вычислить π с 35 десятичными знаками
и завещал вырезать это значение на своем могильном памятнике[53]
(рис. 16).
Рис. 16. Математическая надгробная надпись
Вот оно: 3,14159265358979323846264338327950288…
Некий Шенке в 1873 г. опубликовал такое значение числа я, в котором после запятой следовало 707 десятичных знаков! Такие длинные числа, приближенно выражающие значение я, не имеют ни практической, ни теоретической ценности. Только от безделья да в погоне за дутыми
«рекордами» могло в наше время возникнуть желание «переплюнуть» Шенкса: в 1946–1947 гг. Фергюсон (Манчестерский университет) и
независимо от него Ренч (из Вашингтона) вычислили 808 десятичных знаков для числа π и были польщены тем, что в вычислениях Шенкса обнаружили ошибку начиная с 528 знака.
Если бы мы пожелали, например, вычислить длину земного экватора с точностью до 1 см, предполагая, что знаем длину его диаметра точно, то для этого нам вполне достаточно было бы взять всего 9 цифр после запятой
в числе π . А взяв вдвое больше цифр (18), мы могли бы вычислить длину
окружности, имеющей радиусом расстояние от Земли до Солнца, с погрешностью не свыше 0,0001 мм (в 100 раз меньше толщины волоса!).
Чрезвычайно ярко показал абсолютную бесполезность даже первой сотни десятичных знаков числа п наш соотечественник, математик Граве. Он подсчитал, что если представить себе шар, радиус которого равен расстоянию от Земли до Сириуса, т. е. числу километров равному 132 с десятью нулями: 132 · 1010, наполнить этот шар микробами, полагая в каждом кубическом миллиметре шара по одному биллиону микробов, затем всех этих микробов расположить на прямой линии так, чтобы расстояние между каждыми двумя соседними микробами снова равнялось расстоянию от Сириуса до Земли, то, принимая этот фантастический отрезок за диаметр окружности, можно было бы вычислить длину
получившейся гигантской окружности с микроскопической точностью – до
мм, беря 100 знаков после запятой в числе
π.
Правильно замечает французский астроном Араго, что «в смысле точности мы ничего не выиграли бы, если бы между длиною окружности и
диаметром существовало отношение, выражающееся числом вполне точно».
Для обычных вычислений с числом π вполне достаточно запомнить два знака после запятой (3,14), а для более точных – четыре знака (3,1416: последнюю цифру берем 6 вместо 5 потому, что далее следует цифра, большая 5).
Небольшие стихотворения или яркие фразы дольше остаются в
памяти, чем числа, поэтому для запоминания какого-либо числового значения π придумывают особые стихотворения или отдельные фразы. В произведениях этого вида «математической поэзии» слова подбирают так,
чтобы число букв в каждом слове последовательно совпадало с соответствующей цифрой числа
π.
Известно стихотворение на английском языке – в 13 слов,
следовательно, дающее 12 знаков после запятой в числе
π
; на немецком языке – в 24 слова, а на французском языке в 30 слов[54]
(а есть и в 126 слов!).
Они любопытны, но слишком велики, тяжеловесны. Среди учеников Е.А. Терского – учителя математики одной из средних школ Москвы –
пользуется популярностью придуманная им следующая строфа:
А одна из его учениц – Эся Чериковер – со свойственной нашим школьникам находчивостью сочинила остроумное, слегка ироническое продолжение:
В целом получается такое двустишие из 12 слов:
«Это я знаю и помню прекрасно,
Пи многие знаки мне лишни, напрасны».
Автор этой книги, не отваживаясь на придумывание стихотворения, в свою очередь предлагает простую и тоже вполне достаточную прозаическую фразу: «Что я знаю о кругах?» – вопрос, скрыто заключающий в себе и ответ: 3,1416.
Не может быть, чтобы читатель никогда не слыхал о «квадратуре круга» – о той знаменитейшей задаче геометрии, над которой трудились математики еще 20 веков назад. Я даже уверен, что среди читателей найдутся и такие, которые сами пытались разрешить эту задачу. Еще больше, однако, наберется читателей, которые недоумевают, в чем
собственно кроется трудность этой классической неразрешимой задачи. Многие, привыкшие повторять с чужого голоса, что задача о квадратуре круга неразрешима, не отдают себе ясного отчета ни в сущности самой задачи, ни в трудности ее разрешения.
В математике есть немало задач, гораздо более интересных и теоретически и практически, нежели задача о квадратуре круга. Но ни одна не приобрела такой популярности, как эта проблема, давно вошедшая в
поговорку. Два тысячелетия трудились над ней и выдающиеся математики- профессионалы и несметные толпы любителей.
«Найти квадратуру круга» – значит начертить квадрат, площадь
которого в точности равна площади данного круга. Практически задача эта возникает очень часто, но как раз практически она разрешима с любой точностью. Знаменитая задача древности требует, однако, чтобы чертеж
был выполнен совершенно точно при помощи всего только двух родов
чертежных операций: 1) проведением окружности данного радиуса вокруг
данной точки; 2) проведением прямой линии через две данные точки.
Короче говоря, необходимо выполнить чертеж, пользуясь только двумя чертежными инструментами: циркулем и линейкой.
В широких кругах нематематиков распространено убеждение, что вся трудность обусловлена тем, что отношение длины окружности к ее диаметру (знаменитое число
π)
не может быть выражено конечным числом цифр. Это верно лишь постольку, поскольку неразрешимость задачи зависит от особенной природы числа 71. В самом деле: превращение прямоугольника в квадрат с равной площадью – задача легко и точно разрешимая. Но проблема квадратуры круга сводится ведь к построению –
циркулем и линейкой – прямоугольника, равновеликого данному кругу. Из формулы площади круга, S=πr2, или (что то же самое) S=πr × r, ясно, что площадь круга равна площади такого прямоугольника, одна сторона которого равна r, а другая в π раз больше. Значит, все дело в том, чтобы начертить отрезок, который в π раз длиннее данного. Как известно, я не равно в точности ни З000/7, ни 3,14, ни даже 3,14159. Ряд цифр, выражающих
это число, уходит в бесконечность.
Указанная особенность числа π, его иррациональность (число называется иррациональным, если его нельзя точно выразить дробью вида
, где р и q – целые числа, иррациональные числа выражаются бесконечными непериодическими десятичными дробями) установлена
была еще в XVIII веке математиками Ламбертом и Лежандром, которые непосредственно опирались в этом вопросе на глубокие исследования петербургского академика Эйлера (1707–1783). И все же знание иррациональности я не остановило усилий сведущих в математике
«квадратуристов». Они понимали, что иррациональность π сама по себе не
делает задачи безнадежной. Существуют иррациональные числа, которые
геометрия умеет «строить» совершенно точно. Пусть, например, требуется начертить отрезок, который длиннее данного отрезка в
раз. Число
, как ил, – иррациональное. Тем не менее ничто не может быть легче, чем начертить искомый отрезок: он равен диагонали квадрата,
построенного на данном отрезке.
Каждый школьник легко справляется также и с построением отрезка
(сторона равностороннего вписанного треугольника). Не представляет особых затруднений даже построение такого весьма сложного на вид иррационального выражения
потому что оно сводится к построению правильного 64-угольника.
Как видим, иррациональный множитель, входящий в данное алгебраическое выражение, не всегда делает это выражение невозможным для построения циркулем и линейкой. Неразрешимость квадратуры круга кроется не только в том, что число π – иррациональное, а в другой особенности этого же числа. Именно, число π – не алгебраическое, т. е. оно
не может быть получено в итоге решения какого бы то ни было алгебраического уравнения с рациональными коэффициентами. Такие числа называются трансцендентными.
Французский математик XVI столетия Вьета доказал, что число
Это выражение для я разрешало бы задачу о квадратуре круга, если бы число входящих в него операций было конечно (тогда приведенное
выражение можно было бы геометрически построить). Но так как число извлечений квадратных корней в этом выражении бесконечно, то формула
Вьета не помогает делу.
Итак, неразрешимость задачи о квадратуре круга обусловлена трансцендентностью числа π, т. е. тем, что оно не может получиться в итоге решения алгебраического уравнения с рациональными коэффициентами.
Эта особенность числа
π была строго доказана в 1882 г. немецким математиком Линдеманом. В сущности, названный ученый и должен считаться единственным человеком, разрешившим квадратуру круга,
несмотря на то, что его решение – отрицательное: оно утверждает, что
искомое построение геометрически невыполнимо. Таким образом, в 1882 г.
завершаются многовековые усилия математиков в этом направлении, но, к
сожалению, не прекращаются бесплодные попытки многочисленных
любителей, недостаточно знакомых с историей задачи.
Так обстоит дело с задачей о квадратуре круга в теории. Что касается практики, то она вовсе не нуждается в точном разрешении этой знаменитой задачи. Убеждение многих, что положительное разрешение проблемы о квадратуре круга имело бы огромное значение для практической жизни, – глубокое заблуждение. Для потребностей обихода вполне достаточно располагать хорошими приближенными приемами решения этой задачи.
содержание ..
11
12
13
14 ..

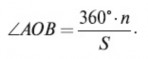

![]()
Загадочное кружение




Измерение голыми руками





Практическая геометрия египтян и римлян

«Это я знаю и помню прекрасно»
![]()

![]()
![]()

![]()
Квадратура круга
![]()
![]()
![]()
![]()

