содержание .. 12 13 14 15 ..
Большая книга занимательных наук (Яков Перельман) - часть 14
Практически поиски квадратуры круга стали бесполезны с того времени, как найдены были первые 7–8 верных цифр числа
π.
Для потребностей практической жизни вполне достаточно знать, что
π
= 3,1415926. Никакое измерение длины не может дать результата, выражающегося более чем семью значащими цифрами. Поэтому брать для
π
более восьми цифр – бесполезно: точность вычисления от этого не улучшается[55]. Если радиус выражен семью значащими цифрами, то длина окружности не будет содержать более семи достоверных цифр, даже если взять для я сотню цифр. То, что старинные математики затратили огромный труд для получения возможно более «длинных» выражений для π, никакого
практического смысла не имеет. Да и научное значение этих трудов ничтожно.
Это – попросту дело терпения. Если у вас есть охота и достаточно досуга, вы можете отыскать хоть 1000 цифр для
π
, пользуясь, например, следующим бесконечным рядом, найденным Лейбницем[56]:
Но это будет никому не нужное арифметическое упражнение, нисколько не изменяющее уже полученного решения знаменитой
геометрической задачи.
Упомянутый ранее французский астроном Араго писал по этому поводу следующее:
«Искатели квадратуры круга продолжают заниматься решением задачи, невозможность которого ныне положительно доказана и которое, если бы даже и могло осуществиться, не представило бы никакого практического интереса. Не стоит распространяться об этом предмете:
больные разумом, стремящиеся к открытию квадратуры круга, не поддаются никаким доводам».
Араго иронически заканчивает:
«Академии всех стран, борясь против искателей квадратуры, заметили,
что болезнь эта обычно усиливается к весне».
Рассмотрим одно из приближенных решений задачи
o квадратуре круга, очень удобное для надобностей практической жизни.
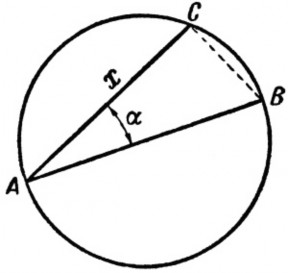
Способ состоит в том, что вычисляют угол а (рис. 17), под которым надо провести к диаметру АВ хорду АС = х, являющуюся стороной искомого квадрата. Чтобы узнать величину этого угла, придется обратиться к тригонометрии:
где r — радиус круга.
Значит, сторона искомого квадрата x = 2r cos α, площадь же его равна 4 r 2cos2α. С другой стороны, площадь квадрата равна r 2 – площади данного круга.
Следовательно,
4 r 2cos2α = π r 2, откуда
По таблицам находим: a = 27°36′.
Итак, проведя в данном круге хорду под углом 27°36′ к диаметру, мы сразу получаем сторону квадрата, площадь которого равна площади
данного круга. Практически для этого заготовляют чертежный треугольник (этот удобный способ был предложен в 1836 г. русским инженером Бингом;
упомянутый чертежный треугольник носит по имени изобретателя
название «треугольник Бинга»), один из острых углов которого 27°36′ (а другой – 62°24′). Располагая таким треугольником, можно для каждого данного круга сразу находить сторону равновеликого ему квадрата.
Рис. 17. Способ русского инженера Бинга (1836 г.)
Для желающих изготовить себе такой чертежный треугольник полезно следующее указание.
Так как тангенс угла 27°36′ равен 0,523, или
, то катеты такого треугольника относятся, как 23:44. Поэтому, изготовив треугольник, один катет которого, например, 22 см, а другой 11,5 см, мы будем иметь то, что требуется. Само собой разумеется, что таким треугольником можно пользоваться и как обыкновенным чертежным.
Поперечный разрез нити, проволоки, даже паутины, как бы мал он ни был, все же имеет определенную геометрическую форму, чаще всего форму
окружности. При этом диаметр поперечного сечения или, будем говорить, толщина одной паутины составляет примерно 5 микронов
мм. Есть ли что-нибудь тоньше паутины? Кто самая искусная
«тонкопряха»? Паук или, может быть, шелковичный червь? Нет. Диаметр нити натурального шелка – 18 микронов, т. е. нить в З000/2 раза толще одной
паутины.
Люди издавна мечтали о том, чтобы своим мастерством превзойти искусство паука и шелковичного червя. Известна старинная легенда об изумительной ткачихе, гречанке Арахнее. Она в таком совершенстве овладела ткацким ремеслом, что ее ткани были тонки, как паутина, прозрачны, как стекло, и легки, как воздух. С ней не могла соперничать даже сама Афина – богиня мудрости и покровительница ремесел.
Эта легенда, как и многие другие древние легенды и фантазии, в наше время стала былью. Искуснее Арахнеи оказались инженеры-химики, создавшие из обыкновенной древесины необычайно тонкое и удивительно прочное искусственное волокно. Шелковые нити, полученные, например,
медноаммиачным промышленным способом, в 2000/2 раза тоньше паутины, а в прочности почти не уступают нитям натурального шелка. Натуральный шелк выдерживает нагрузку до 30 кг на 1 кв. мм поперечного сечения, а медноаммиачный – до 25 кг на 1 кв. мм.
Любопытен способ изготовления медноаммиачного шелка. Древесину превращают в целлюлозу, а целлюлозу растворяют в аммиачном растворе
меди. Струйки раствора через тонкие отверстия выливают в воду, вода отнимает растворитель, после чего образующиеся нити наматывают на соответствующие приспособления. Толщина нити медноаммиачного шелка
– 2 микрона. На 1 микрон толще ее так называемый ацетатный, тоже искусственный, шелк. Поразительно то, что некоторые сорта ацетатного шелка крепче стальной проволоки! Если стальная проволока выдерживает
нагрузку в 110 кг на один квадратный миллиметр поперечного сечения, то нить ацетатного шелка выдерживает 126 кг на 1 кв. мм.
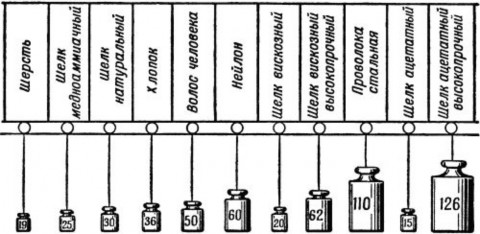
Рис. 18. Сравнительная толщина волокон
Всем вам хорошо известный вискозный шелк имеет толщину нити около 4 микронов, а предельную прочность от 20 до 62 кг на 1 кв. мм
поперечного сечения. На рис. 18 приведена сравнительная толщина
паутины, человеческого волоса, различных искусственных волокон, а также волокон шерсти и хлопка, а на рис. 19 – их крепость в килограммах на 1 кв. мм. Искусственное или, как его еще называют, синтетическое волокно – одно из крупнейших современных технических открытий, имеющее огромное хозяйственное значение. Вот что рассказывает инженер Буянов:
«Хлопок растет медленно, и количество его зависит от климата и урожая. Производитель натурального шелка – шелковичный червь – чрезвычайно ограничен в своих возможностях. За свою жизнь он выпрядет кокон, в котором имеется лишь 0,5 г шелковой нити…
Рис. 19. Предельная прочность волокон (в кг на 1 кв. мм поперечного сечения)
Количество искусственного шелка, полученного путем химической
переработки из 1 куб. м древесины, заменяет 320 000 шелковых коконов или годовой настриг шерсти с 30 овец, или средний урожай хлопка с 000/2 га. Этого количества волокон достаточно для выработки четырех тысяч пар женских чулок или 1500 м шелковой ткани».
Еще хуже представляем мы себе большое и малое в геометрии, где приходится сравнивать не числа, а поверхности и объемы. Каждый, не
задумываясь, ответит, что 5 кг варенья больше, чем 3 кг, но не всегда сразу скажет, которая из двух банок, стоящих на столе, вместительнее.
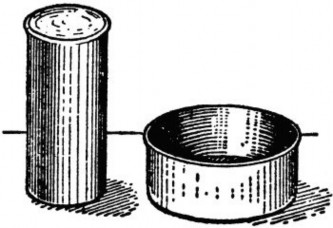
ЗАДАЧА Которая из двух банок (рис. 20) вместительнее – правая, широкая, или левая, втрое более высокая, но вдвое более узкая?
РЕШЕНИЕ
Для многих, вероятно, будет неожиданностью, что в нашем случае
высокая банка менее вместительна, нежели широкая. Между тем легко проверить это расчетом.
Рис. 20. Которая банка вместительнее?
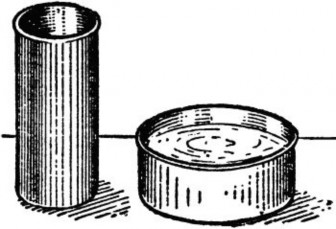
Рис. 21. Результат переливания содержимого высокой банки в широкую
Площадь основания широкой банки в 2 х 2, т. е. в четыре раза больше,
чем узкой; высота же ее всего в три раза меньше. Значит, объем широкой
банки в 4/3 раза больше, чем узкой. Если содержимое высокой банки перелить в широкую, оно заполнит лишь 3/4 ее объема (рис. 21).
ЗАДАЧА
В витрине табачного треста выставлена огромная папироса, в 15 раз длиннее и в 15 раз толще обыкновенной. Если на набивку одной папиросы
нормальных размеров нужно полграмма табаку, то сколько табаку
понадобилось, чтобы набить исполинскую папиросу, показанную в
витрине?
РЕШЕНИЕ
т. е. свыше 1000/2 кг.
«Потому что они легче воздуха», – вот обычный ответ, который представляется многим до того бесспорным, что не оставляет никаких поводов к сомнению. Но такое объяснение при его подкупающей простоте
совершенно ошибочно. Пылинки не только не легче воздуха, но они тяжелее его в сотни и даже тысячи раз.
Что такое «пылинки»? Мельчайшие частицы различных тяжелых тел: осколки камня или стекла, крупинки угля, дерева, металлов, волокна тканей
и т. п. Разве все эти материалы легче воздуха? Простая справка в таблице удельных весов убедит вас, что каждый из них либо в несколько раз тяжелее воды, либо легче ее всего в два-три раза. А вода тяжелее воздуха раз в 800; следовательно, пылинки тяжелее его в несколько сот, если не тысяч раз. Теперь очевидна вся несообразность ходячего взгляда на причину плавания пылинок в воздухе.
Какова же истинная причина? Прежде всего, надо заметить, что обычно мы неправильно представляем себе самое явление, рассматривая его как плавание. Плавают – в воздухе (или жидкости) – только такие тела, вес которых не превышает веса равного объема воздуха (или жидкости). Пылинки же превышают этот вес во много раз, поэтому плавать в воздухе они не могут. Они и не плавают, а парят, т. е. медленно опускаются, задерживаемые в своем падении сопротивлением воздуха. Падающая
пылинка должна проложить себе путь между частицами воздуха, расталкивая их или увлекая с собой. На то и другое расходуется энергия падения. Расход тем значительнее, чем больше поверхность тела (точнее –
площадь поперечного сечения) по сравнению с весом. При падении крупных, массивных тел мы не замечаем замедляющего действия сопротивления воздуха, так как их вес значительно преобладает над
противодействующей силой.
Но посмотрим, что происходит при уменьшении тела. Геометрия поможет нам разобраться в этом. Нетрудно сообразить, что с уменьшением
объема тела вес уменьшается гораздо больше, чем площадь поперечного сечения: уменьшение веса пропорционально третьей степени линейного сокращения, а ослабление сопротивления пропорционально поверхности, т. е. второй степени линейного уменьшения.
Какое это имеет значение в нашем случае, ясно из следующего примера. Возьмем крокетный шар диаметром в 10 см и крошечный шарик из того же материала диаметром в 1 мм. Отношение их линейных размеров равно 100, потому что 10 см больше одного миллиметра в 100 раз. Маленький шарик легче крупного в 1003 раз, т. е. в миллион раз; сопротивление же, встречаемое им при движении в воздухе, слабее только в
1002 раз, т. е. в десять тысяч раз. Ясно, что маленький шарик должен падать медленнее крупного. Короче говоря, причиной того, что пылинки держатся в воздухе, является их «парусность», обусловленная малыми размерами, а вовсе не то, что они будто бы легче воздуха. Водяная капелька радиусом 0,001 мм падает в воздухе равномерно со скоростью 0,1 мм в секунду; достаточно ничтожного, неуловимого для нас течения воздуха,
чтобы помешать такому медленному падению.
Вот почему в комнате, где много ходят, пыли осаждается меньше, чем в нежилых помещениях, и днем меньше, чем ночью, хотя, казалось бы, должно происходить обратное: осаждению мешают возникающие в воздухе вихревые течения, которых обычно почти не бывает в спокойном воздухе мало посещаемых помещений.
Если каменный кубик в 1 см высотой раздробить на кубические пылинки высотой в 0,0001 см, то общая поверхность той же массы камня увеличится в 10 000 раз и во столько же раз возрастет сопротивление воздуха ее движению. Пылинки нередко достигают именно таких размеров, и понятно, что сильно возросшее сопротивление воздуха совершенно меняет картину падения.
По той же причине «плавают» в воздухе облака. Давно отвергнут устарелый взгляд, будто облака состоят из водяных пузырьков, наполненных водяным паром. Облака – скопление огромного множества
чрезвычайно мелких, но сплошных водяных капелек. Капельки эти, хотя тяжелее воздуха раз в 800, все же почти не падают; они опускаются с едва заметной скоростью. Сильно замедленное падение объясняется, как и для пылинок, огромной их поверхностью по сравнению с весом.
Самый слабый восходящий поток воздуха способен поэтому не только
прекратить крайне медленное падение облаков, поддерживая их на определенном уровне, но и поднять их вверх.
Главная причина, обусловливающая все эти явления, – присутствие
воздуха: в пустоте и пылинки и облака (если бы могли существовать) падали бы столь же стремительно, как и тяжелые камни.
Излишне добавлять, что медленное падение человека с парашютом (около 5 м/сек) принадлежит к явлениям подобного же порядка.
Задача Льва Толстого
Эту главу, необычное название которой станет понятным читателю из дальнейшего, начнем отрывком из общеизвестного рассказа Л.H. Толстого
«Много ли человеку земли нужно».
«– А цена какая будет? – говорит Пахом.
Цена у нас одна: 1000 руб. за день. Не понял Пахом.
Какая же это мера – день? Сколько в ней десятин будет?
Мы этого, – говорит, – не умеем считать. А мы за день продаем; сколько обойдешь в день, то и твое, а цена 1000 руб.
Удивился Пахом.
Да ведь это, – говорит, – в день обойти земли много будет. Засмеялся старшина.
Вся твоя, – говорит. – Только один уговор, если назад не придешь в день к тому месту, с какого возьмешься, пропали твои деньги.
А как же, – говорит Пахом, – отметить, где я пройду?
А мы станем на место, где ты облюбуешь; мы стоять будем, а ты иди, делай круг, а с собой скребку возьми и, где надобно, замечай, на углах ямки
рой, дерничка клади; потом с ямки на ямку плугом пройдем. Какой хочешь круг забирай, только до захода солнца приходи к тому месту, с какого взялся. Что обойдешь, все твое.
Разошлись башкирцы. Обещались завтра на зорьке собраться, до солнца на место выехать.
Приехали в степь, заря занимается. Подошел старшина к Пахому, показал рукой.
Вот, – говорит, – все наше, что глазом окинешь. Выбирай любую.
Снял старшина шапку лисью, поставил на землю.
Вот, – говорит, – метка будет. Отсюда поди, сюда приходи. Что обойдешь, все твое будет.
Только брызнуло из-за края солнце, вскинул Пахом скребку на плечо и
пошел в степь.
Отошел с версту, остановился, вырыл ямку. Пошел дальше. Отошел еще, вырыл еще другую ямку.
Верст 5 прошел. Взглянул на солнышко, – уже время об завтраке.
«Одна упряжка прошла, – думает Пахом. – А их четыре во дню, рано еще заворачивать. Дай пройду еще верст пяток, тогда влево загибать начну». Пошел еще напрямик.
«Ну, – думает, – в эту сторону довольно забрал; надо загибать».
Остановился, вырыл ямку побольше и загнул круто влево.
Прошел еще и по этой стороне много; загнул второй угол. Оглянулся
Пахом на шихан (бугорок): от тепла затуманился, а сквозь мару чуть виднеются люди на шихане. «Ну, – думает, – длинны стороны взял, надо эту покороче взять». Пошел третью сторону. Посмотрел на солнце, – уж оно к полднику подходит, а по третьей стороне всего версты две прошел. И до места все те же верст 15. «Нет, – думает, – хоть кривая дача будет, а надо прямиком поспевать».
Вырыл Пахом поскорее ямку и повернул прямиком к шихану.
Идет Пахом прямо на шихан, и тяжело уж ему стало. Отдохнуть хочется, а нельзя, – не поспеешь дойти до заката. А солнце уж недалеко от края.
Идет так Пахом; трудно ему, а все прибавляет да прибавляет шагу. Шел, шел – все еще далеко; побежал рысью… Бежит Пахом, рубаха и
портки от пота к телу липнут, во рту пересохло. В груди как меха кузнечные раздуваются, а сердце молотком бьет.
Бежит Пахом из последних сил, а солнце уж к краю подходит. Вот-вот закатываться станет.
Солнце близко, да и место уж вовсе недалеко. Видит шапку лисью на земле и старшину, как он на земле сидит.
Взглянул Пахом на солнце, а оно до земли дошло, уже краешком заходить стало. Наддал из последних сил Пахом, надулся, взбежал на шихан. Видит – шапка. Подкосились ноги, и упал он наперед руками, до
шапки достал.
– Ай, молодец! – закричал старшина, – много земли завладел.
Подбежал работник, хотел поднять его, а у него изо рта кровь течет, и он мертвый лежит…»
Отвлечемся от мрачной развязки этой истории и остановимся на ее геометрической стороне. Можно ли установить по данным, рассеянным в
этом рассказе, сколько примерно десятин земли обошел Пахом? Задача – на
первый взгляд как будто невыполнимая – решается, однако, довольно просто.
РЕШЕНИЕ
Внимательно перечитывая рассказ и извлекая из него все геометрические указания, нетрудно убедиться, что полученных данных вполне достаточно для исчерпывающего ответа на поставленный вопрос. Можно даже начертить план обойденного Пахомом земельного участка.
Прежде всего из рассказа ясно, что Пахом бежал по сторонам четырехугольника. О первой стороне его читаем:
«Верст пять прошел… Пройду еще верст пяток; тогда влево
загибать…».
Значит, первая сторона четырехугольника имела в длину около 10 верст.
О второй стороне, составляющей прямой угол с первой, численных указаний в рассказе не сообщается.
Длина третьей стороны – очевидно, перпендикулярной ко второй, –
указана в рассказе прямо:
«По третьей стороне всего версты две прошел».
Непосредственно дана и длина четвертой стороны:
«До места все те же верст 15»[57].
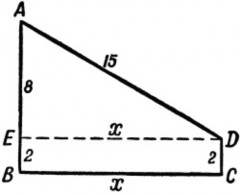
По этим данным мы и можем начертить план обойденного Пахомом участка (рис. 22). В полученном четырехугольнике ABCD сторона АВ = 10 верстам, CD = 2 верстам, AD = 15 верстам; углы В и С – прямые. Длину х неизвестной стороны ВС нетрудно вычислить, если провести из
D перпендикуляр
DE
к АВ
(рис. 23). Тогда в прямоугольном треугольнике
AED нам известны катет
АЕ
= 8 верстам и гипотенуза
AD =15 верстам.
Неизвестный катет
верстам.
Итак, вторая сторона имела в длину около 13 верст. Очевидно, Пахом
ошибся, считая вторую сторону короче первой.
Как видите, можно довольно точно начертить план того участка, который обежал Пахом. Несомненно, Л.H. Толстой имел перед глазами
чертеж наподобие рис. 22, когда писал свой рассказ.
Рис. 22. Маршрут Пахома
Рис. 23. Уточнение маршрута
Теперь легко вычислить и площадь трапеции ABCD, состоящей из прямоугольника EBCD и прямоугольного треугольника АED . Она равна
Вычисление по формуле трапеции дало бы, конечно, тот же результат:
Мы узнали, что Пахом обежал обширный участок площадью в 78 кв. верст, или около 8000 десятин. Десятина обошлась бы ему в 12 000/2 копеек.
ЗАДАЧА
В роковой для своей жизни день Пахом прошел 10+13+2+15 = 40
верст, идя по сторонам трапеции. Его первоначальным намерением было
идти по сторонам прямоугольника; трапеция же получилась случайно, в
результате плохого расчета. Интересно определить: выгадал ли он или прогадал от того, что участок его оказался не прямоугольником, а трапецией? В каком случае должен он был получить большую площадь земли?
РЕШЕНИЕ
Прямоугольников с обводом в 40 верст может быть очень много, и каждый имеет другую площадь. Вот ряд примеров:
14 × 6 = 84 кв. верст
13 × 7 = 91»»
12 × 8 = 96»»
11 × 9 = 99»»
Мы видим, что у всех этих фигур при одном и том же периметре в 40 верст площадь больше, чем у нашей трапеции. Однако возможны и такие прямоугольники с периметром в 40 верст, площадь которых меньше, чем у трапеции:
Следовательно, на вопрос задачи нельзя дать определенного ответа. Есть прямоугольники с большей площадью, чем трапеция, но есть и с меньшей, при одном и том же обводе. Зато можно дать вполне определенный ответ на вопрос: какая из всех прямоугольных фигур с заданным периметром заключает самую большую площадь? Сравнивая
наши прямоугольники, мы замечаем, что чем меньше разница в длине сторон, тем площадь прямоугольника больше. Естественно заключить, что
когда этой разницы не будет вовсе, т. е. когда прямоугольник превратится в
квадрат, площадь фигуры достигнет наибольшей величины. Она будет равна тогда 10 х 10 = 100 кв. верст.
Легко видеть, что этот квадрат действительно превосходит по площади
любой прямоугольник одинакового с ним периметра. Пахому следовало идти по сторонам квадрата, чтобы получить участок наибольшей площади
– на 22 кв. версты больше, чем он успел охватить.
Замечательное свойство квадрата – заключать в своих границах наибольшую площадь по сравнению со всеми другими прямоугольниками того же периметра – многим неизвестно. Приведем поэтому строгое доказательство этого положения.
Обозначим периметр прямоугольной фигуры через Р. Если взять квадрат с таким периметром, то каждая сторона его должна равняться
. Докажем, что, укорачивая одну его сторону на какую-нибудь величину b при таком же удлинении смежной стороны, мы получим
прямоугольник одинакового с ним периметра, но меньшей площади.
Другими словами, докажем, что площадь
квадрата больше площади
прямоугольника:
Так как правая сторона этого неравенства равна
, то все выражение принимает вид 0 > – b 2, или b 2 > 0.
Но последнее неравенство очевидно: квадрат всякого количества,
положительного или отрицательного, больше 0. Следовательно, справедливо и первоначальное неравенство, которое привело нас к этому.
Итак, квадрат имеет наибольшую площадь из всех прямоугольников с
таким же периметром.
Отсюда следует, между прочим, и то, что из всех прямоугольных
фигур с одинаковыми площадями квадрат имеет наименьший периметр. В
этом можно убедиться следующим рассуждением. Допустим, что это
неверно и что существует такой прямоугольник А, который при равной с
квадратом В площади имеет периметр меньший, чем у него. Тогда, начертив квадрат С того же периметра, как у прямоугольника А, мы получим квадрат, имеющий бо́льшую площадь, чем у А, и, следовательно, большую, чем у квадрата В. Что же у нас вышло? Что квадрат С имеет периметр меньший, чем квадрат В, а площадь большую, чем он. Это очевидно невозможно: раз сторона квадрата С меньше, чем сторона квадрата В, то и площадь должна быть меньше. Значит, нельзя было допустить существование прямоугольника А, который при одинаковой площади имеет периметр меньший, чем у квадрата. Другими словами, из всех прямоугольников с одинаковой площадью наименьший периметр
имеет квадрат.
Знакомство с этими свойствами квадрата помогло бы Пахому правильно рассчитать свои силы и получить прямоугольный участок наибольшей площади. Зная, что он может пройти в день без напряжения, скажем, 36 верст, он пошел бы по границе квадрата со стороной 9 верст и к вечеру был бы обладателем участка в 81 кв. версту, – на 3 кв. версты
больше, чем он получил со смертельным напряжением сил. И, наоборот, если бы он наперед ограничился какой-нибудь определенной площадью прямоугольного участка, например в 36 кв. верст, то мог бы достичь результата с наименьшей затратой сил, идя по границе квадрата, сторона которого – 6 верст.
содержание ..
12
13
14
15 ..
![]()
![]()
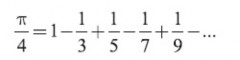
Треугольник Бинга

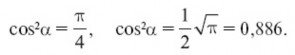
![]()
Тоньше паутины, но крепче стали
![]()

Две банки
Исполинская папироса

Почему пыль и облака плавают в воздухе?
Как Пахом покупал землю
![]()
![]()



Трапеция или прямоугольник?
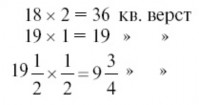
Замечательное свойство квадрата
![]()
![]()


