Physics For Scientists And Engineers 6E - part 39

SECTION 6.1 •  Newton’s Second Law Applied to Uniform Circular Motion

153

Conceptual Example 6.1 Forces That Cause Centripetal Acceleration

The  force  causing  centripetal  acceleration  is  sometimes
called  a  centripetal  force. We  are  familiar  with  a  variety  of
forces  in  nature—friction,  gravity,  normal  forces,  tension,
and so forth. Should we add centripetal force to this list?

Solution No;  centripetal  force  should  not be  added  to  this
list. This is a pitfall for many students. Giving the force caus-
ing circular motion a name—centripetal force—leads many
students to consider it as a new kind of force rather than a
new role for force. A common mistake in force diagrams is to
draw all the usual forces and then to add another vector for
the centripetal force. But it is not a separate force—it is sim-
ply one or more of our familiar forces acting in the role of a
force that causes a circular motion.

Consider  some  examples.  For  the  motion  of  the  Earth

around  the  Sun,  the  centripetal  force  is  gravity. For  an  ob-
ject  sitting  on  a  rotating  turntable,  the  centripetal  force  is
friction. For  a  rock  whirled  horizontally  on  the  end  of  a
string, the magnitude of the centripetal force is the tension
in the string. For an amusement-park patron pressed against
the  inner  wall  of  a  rapidly  rotating  circular  room,  the  cen-
tripetal force is the normal force exerted by the wall. Further-
more,  the  centripetal  force  could  be  a  combination  of  two
or more forces. For example, as you pass through the lowest
point of the Ferris wheel in Quick Quiz 6.1, the centripetal
force on you is the difference between the normal force ex-
erted by the seat and the gravitational force. We will not use
the term centripetal force in this book after this discussion.

Example 6.3 How Fast Can It Spin?

A  ball  of  mass  0.500 kg  is  attached  to  the  end  of  a  cord
1.50 m  long.  The  ball  is  whirled  in  a  horizontal  circle  as
shown in Figure 6.1. If the cord can withstand a maximum
tension of 50.0 N, what is the maximum speed at which the
ball can be whirled before the cord breaks? Assume that the
string remains horizontal during the motion.

Solution It  makes  sense  that  the  stronger  the  cord,  the
faster the ball can twirl before the cord breaks. Also, we ex-
pect a more massive ball to break the cord at a lower speed.
(Imagine whirling a bowling ball on the cord!)

Because the force causing the centripetal acceleration in

this  case  is  the  force  T exerted  by  the  cord  on  the  ball,

Equation 6.1 yields 

Solving for v, we have

This shows that v increases with T and decreases with larger
m, as we expect to see—for a given v, a large mass requires a
large  tension  and  a  small  mass  needs  only  a  small  tension.
The maximum speed the ball can have corresponds to the

v !

√

Tr

m

(1)

            T ! m 

 

v

 

 

2

r

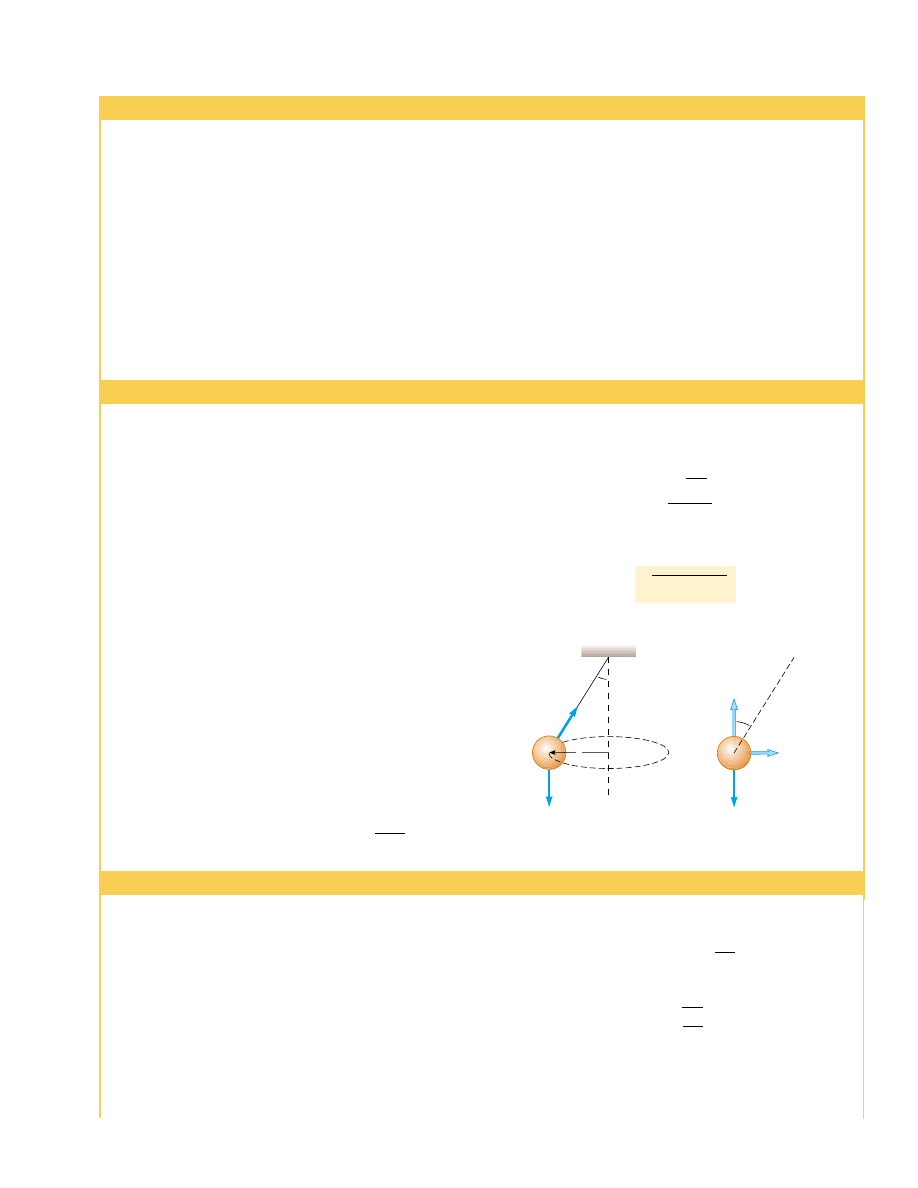
Example 6.2 The Conical Pendulum

A  small  object  of  mass  m is  suspended  from  a  string  of
length L. The object revolves with constant speed v in a hor-
izontal  circle  of  radius  r, as  shown  in  Figure  6.4.  (Because
the  string  sweeps  out  the  surface  of  a  cone,  the  system  is
known as a conical pendulum.) Find an expression for v.

Solution Conceptualize  the  problem  with  the  help  of  Fig-
ure 6.4. We categorize this as a problem that combines equi-
librium  for  the  ball  in  the  vertical  direction  with  uniform
circular  motion  in  the  horizontal  direction.  To  analyze  the
problem,  begin  by  letting  " represent  the  angle  between
the string and the vertical. In the free-body diagram shown,
the  force 

T exerted by the string is resolved into a vertical

component T cos " and a horizontal component T sin " act-
ing toward the center of revolution. Because the object does
not  accelerate  in  the  vertical  direction,  F

y

!

ma

y

!

0  and

the upward vertical component of 

T must balance the down-

ward gravitational force. Therefore,

Because the force providing the centripetal acceleration in
this example is the component T sin ", we can use Equation
6.1 to obtain

(2)

     

!

 F ! T

  

sin

 

" !

ma

c

!

mv

 

2

r

(1)

     

T

  

cos

 

" !

mg

!

Dividing (2) by (1) and using sin "/cos " ! tan ", we elimi-
nate T and find that

From  the  geometry  in  Figure  6.4,  we  see  that  r ! L sin ";
therefore,

v !

Note that the speed is independent of the mass of the object.

√

Lg

  

sin

  

"

  

tan

 

"

v !

√

r

 

g

  

tan

 

"

tan

 

" !

v

 

2

r

 

g

T

mg

T cos

mg

T sin

r

θ

θ

θ

θ

L

Figure 6.4 (Example 6.2) The conical pendulum and its free-

body diagram.

154

CHAPTE R 6 •  Circular Motion and Other Applications of Newton’s Laws

Example 6.4 What Is the Maximum Speed of the Car?

A 1 500-kg car moving on a flat, horizontal road negotiates a
curve,  as  shown  in  Figure  6.5.  If  the  radius  of  the  curve  is
35.0 m and the coefficient of static friction between the tires
and dry pavement is 0.500, find the maximum speed the car
can have and still make the turn successfully.

Solution In this case, the force that enables the car to re-
main in its circular path is the force of static friction. (Static
because no slipping occurs at the point of contact between
road and tires. If this force of static friction were zero—for
example, if the car were on an icy road—the car would con-
tinue in a straight line and slide off the road.) Hence, from
Equation 6.1 we have

(1)

            f

s

!

m

 

v

 

2

r

The maximum speed the car can have around the curve is the
speed at which it is on the verge of skidding outward. At this
point, the friction force has its maximum value f

s, max

!

#

s

n.

Because the car shown in Figure 6.5b is in equilibrium in the
vertical  direction,  the  magnitude  of  the  normal  force  equals
the weight (n ! mg) and thus f

s, max

!

#

s

mg. Substituting this

value for f

s

into (1), we find that the maximum speed is

!

Note that the maximum speed does not depend on the mass
of the car. That is why curved highways do not need multi-
ple speed limit signs to cover the various masses of vehicles
using the road.

What If?

Suppose that a car travels this curve on a wet day

and begins to skid on the curve when its speed reaches only
8.00 m/s. What can we say about the coefficient of static fric-
tion in this case?

Answer The  coefficient  of  friction  between  tires  and  a  wet
road should be smaller than that between tires and a dry road.
This expectation is consistent with experience with driving, be-
cause a skid is more likely on a wet road than a dry road.

To check our suspicion, we can solve (2) for the coeffi-

cient of friction:

Substituting the numerical values,

This is indeed smaller than the coefficient of 0.500 for the
dry road.

#

s

!

v

 

2

max

g

 

r

!

(8.00 m/s)

2

(9.80 m/s

2

)(35.0 m)

!

0.187

#

s

!

v

max

 

2

g

 

r

13.1

  m/s

!

√

(0.500)(9.80 m/s

2

)(35.0 m)

(2)

            v

 

max 

!

√

f

s

 

, max

 r

m

!

√

#

s

m

 

g

 

r

m

!

√

#

s

 

g

 

r

n

mg

(a)

(b)

f 

s

f 

s

Figure 6.5 (Example 6.4) (a) The force of static friction di-

rected toward the center of the curve keeps the car moving in a

circular path. (b) The free-body diagram for the car.

Study the relationship between the car’s speed, radius of the turn, and the coefficient of static friction between road and
tires at the Interactive Worked Example link at http://www.pse6.com.

Interactive

maximum tension. Hence, we find

!

What  If?

Suppose  that  the  ball  is  whirled  in  a  circle  of

larger radius at the same speed v. Is the cord more likely to
break or less likely?

Answer The larger radius means that the change in the di-
rection of the velocity vector will be smaller for a given time
interval. Thus, the acceleration is smaller and the required
force from the string is smaller. As a result, the string is less
likely  to  break  when  the  ball  travels  in  a  circle  of  larger
radius.  To  understand  this  argument  better,  let  us  write

12.2 m/s

v

 

max 

!

√

T

 

max

r

m

!

√

(50.0 N) (1.50 m)

0.500 kg

Equation (1) twice, once for each radius:

Dividing the two equations gives us,

If we choose r

2

$

r

1

, we see that T

2

%

T

1

. Thus, less tension

is  required  to  whirl  the  ball  in  the  larger  circle  and  the
string is less likely to break.

T

2

T

1

!

"

mv

2

r

2

#

"

mv

2

r

1

#

!

r

 

1

r

 

2

T

1

!

mv

 

2

r

 

1

        T

2

!

mv

 

2

r

 

2

SECTION 6.1 •  Newton’s Second Law Applied to Uniform Circular Motion

155

Example 6.5 The Banked Exit Ramp

A civil engineer wishes to design a curved exit ramp for a
highway  in  such  a  way  that  a  car  will  not  have  to  rely  on
friction  to  round  the  curve  without  skidding.  In  other
words, a car moving at the designated speed can negotiate
the  curve  even  when  the  road  is  covered  with  ice.  Such  a
ramp is usually banked; this means the roadway is tilted to-
ward the inside of the curve. Suppose the designated speed
for the ramp is to be 13.4 m/s (30.0 mi/h) and the radius
of the curve is 50.0 m. At what angle should the curve be
banked?

Solution On a level (unbanked) road, the force that causes
the centripetal acceleration is the force of static friction be-
tween  car  and  road,  as  we  saw  in  the  previous  example.
However,  if  the  road  is  banked  at  an  angle  ",  as  in  Figure
6.6, the normal force n has a horizontal component n sin "
pointing toward the center of the curve. Because the ramp
is to be designed so that the force of static friction is zero,
only  the  component  n

x

!

n sin " causes  the  centripetal

acceleration. Hence, Newton’s second law for the radial di-
rection gives

The  car  is  in  equilibrium  in  the  vertical  direction.  Thus,
from  F

y

!

0 we have

Dividing (1) by (2) gives

If a car rounds the curve at a speed less than 13.4 m/s, fric-
tion is needed to keep it from sliding down the bank (to the
left in Fig. 6.6). A driver who attempts to negotiate the curve
at a speed greater than 13.4 m/s has to depend on friction
to keep from sliding up the bank (to the right in Fig. 6.6).
The banking angle is independent of the mass of the vehicle
negotiating the curve.

What  If?

What  if  this  same  roadway  were  built  on  Mars  in

the  future  to  connect  different  colony  centers;  could  it  be
traveled at the same speed?

Answer The  reduced  gravitational  force  on  Mars  would
mean  that  the  car  is  not  pressed  so  tightly  to  the  roadway.
The  reduced  normal  force  results  in  a  smaller  component
of  the  normal  force  toward  the  center  of  the  circle.  This
smaller component will not be sufficient to provide the cen-
tripetal acceleration associated with the original speed. The
centripetal  acceleration  must  be  reduced,  which  can  be
done by reducing the speed v.

Equation  (3)  shows  that  the  speed  v is  proportional  to

the square root of g for a roadway of fixed radius r banked at
a  fixed  angle  ".  Thus,  if  g is  smaller,  as  it  is  on  Mars,  the
speed v with which the roadway can be safely traveled is also
smaller.

20.1&

" !

tan

'

1

"

(13.4 m/s)

2

(50.0 m)(9.80 m/s

2

)

#

!

(3)

            tan

 

" !

v

 

2

r

 

g

(2)

            n

  

cos

 

" !

mg

!

(1)

           

!

 

F

r

!

n

  

sin

 

" !

mv

 

2

r

n

n

x

n

y

F

g

θ

Figure 6.6 (Example 6.5) A car rounding a curve on a road

banked at an angle 

"

to the horizontal. When friction is ne-

glected, the force that causes the centripetal acceleration and

keeps the car moving in its circular path is the horizontal com-

ponent of the normal force.

You can adjust the turn radius and banking angle at the Interactive Worked Example link at http://www.pse6.com.

Example 6.6 Let’s Go Loop-the-Loop!

A pilot of mass m in a jet aircraft executes a loop-the-loop,
as  shown  in  Figure  6.7a.  In  this  maneuver,  the  aircraft
moves  in  a  vertical  circle  of  radius  2.70 km  at  a  constant
speed of 225 m/s. Determine the force exerted by the seat
on  the  pilot 

(A)

at  the  bottom  of  the  loop  and 

(B)

at  the

top of the loop. Express your answers in terms of the weight
of the pilot mg.

Solution To  conceptualize  this  problem,  look  carefully  at
Figure  6.7.  Based  on  experiences  with  driving  over  small

hills in a roadway, or riding over the top of a Ferris wheel,
you would expect to feel lighter at the top of the path. Simi-
larly, you would expect to feel heavier at the bottom of the
path.  By  looking  at  Figure  6.7,  we  expect  the  answer  for
(A) to be greater than that for (B) because at the bottom of
the  loop  the  normal  and  gravitational  forces  act  in  opposite
directions,  whereas  at  the  top  of  the  loop  these  two  forces
act in the same direction. The vector sum of these two forces
gives  the  force  of  constant  magnitude  that  keeps  the  pilot
moving in a circular path at a constant speed. To yield net

Interactive

156

CHAPTE R 6 •  Circular Motion and Other Applications of Newton’s Laws

force vectors with the same magnitude, the normal force at
the  bottom  must  be  greater  than  that  at  the  top.  Because
the speed of the aircraft is constant (how likely is this?), we
can  categorize  this  as  a  uniform  circular  motion  problem,
complicated by the fact that the gravitational force acts at all
times on the aircraft. 

(A)

Analyze the situation by drawing a free-body diagram for

the pilot at the bottom of the loop, as shown in Figure 6.7b.
The only forces acting on him are the downward gravitational
force 

F

g

!

m

g and the upward force n

bot

exerted by the seat.

Because the net upward force that provides the centripetal ac-
celeration  has  a  magnitude  n

bot

'

mg,  Newton’s  second  law

for the radial direction gives

Substituting the values given for the speed and radius gives

Hence, the magnitude of the force n

bot

exerted by the seat

on the pilot is greater than the weight of the pilot by a fac-
tor of 2.91. This means that the pilot experiences an appar-

2.91mg

n

bot

!

mg

 

"

1 (

(225 m/s)

2

(2.70 ) 10

3 

m)(9.80 m/s

2

)

#

!

n

bot

!

mg ( m

v

 

2

r

!

mg

"

1 (

v

 

2

r

 

g

#

!

 

F ! n

 

bot

'

mg ! m 

v

2

r

ent  weight  that  is  greater  than  his  true  weight  by  a  factor
of 2.91. 

(B)

The  free-body  diagram  for  the  pilot  at  the  top  of  the

loop is shown in Figure 6.7c. As we noted earlier, both the
gravitational  force  exerted  by  the  Earth  and  the  force 

n

top

exerted  by  the  seat  on  the  pilot  act  downward,  and  so  the
net  downward  force  that  provides  the  centripetal  accelera-
tion has a magnitude n

top

(

mg. Applying Newton’s second

law yields

!

In this case, the magnitude of the force exerted by the seat
on the pilot is less than his true weight by a factor of 0.913,
and the pilot feels lighter. To finalize the problem, note that
this is consistent with our prediction at the beginning of the
solution.

0.913mg

n

 

top

!

mg

"

(225 m/s)

2

(2.70 ) 10

3

 m)(9.80 m/s

2

)

'

1

#

n

top

!

m 

v

 

2

r

  ' mg ! mg

"

v

 

2

rg

'

1

#

!

 

F ! n

top

(

mg ! m  

v

2

r

n

bot

mg

n

top

mg

(b)

(c)

Top

Bottom

A

(a)

Figure 6.7 (Example 6.6) (a) An aircraft executes a loop-the-loop maneuver as it

moves in a vertical circle at constant speed. (b) Free-body diagram for the pilot at the

bottom of the loop. In this position the pilot experiences an apparent weight greater

than his true weight. (c) Free-body diagram for the pilot at the top of the loop.