Вариант экзаменационных билетов по теоретической механике
СЛОВАРЬ
ТЕРМИНОВ, ОПРЕДЕЛЕНИЙ, ПОНЯТИЙ
Механика – наука о механическом движении и механическом взаимодействии материальных тел.
Теоретическая механика – раздел механики, в котором изучаются законы движения механических систем и общие свойства этих движений.
Статика – раздел механики, в котором изучаются условия равновесия механических систем под действием сил.
Кинематика – раздел теоретической механики, в котором изучаются движения материальных тел без учёта их масс и действующих на них сил.
Динамика – раздел механики, в котором изучаются движения механических систем под действием сил.
Масса – одна из основных характеристик любого материального объекта, определяющая его инертные и гравитационные свойства.
Инертность – свойство материального тела, проявляющееся в сохранении движения, совершаемого им при отсутствии действующих сил, и в постепенном изменении этого движения с течением времени, когда на тело начинают действовать силы.
Материальная точка – точка, имеющая массу.
Абсолютно твёрдое тело – материальное тело, в котором расстояние между двумя любыми точками остается неизменным.
Механическая система – любая совокупность материальных точек, движения которых взаимозависимы.
Механическое действие – действие на данное тело со стороны других тел, которое приводит к изменению скоростей точек этого тела или следствием которого является изменение взаимного положения точек данного тела.
Механическое движение – изменение с течением времени взаимного положения в пространстве материальных тел или взаимного положения частей данного тела.
Свободное твёрдое тело – тело, на перемещения которого не наложено никаких ограничений.
Система отсчёта – система координат, связанная с телом, по отношению к которому определяется положение других тел (механических систем) в разные моменты времени.
Сила – векторная величина, являющаяся мерой механического действия одного тела на другое.
Сила тяжести – сила, действующая на точку вблизи земной поверхности, равная произведению массы m этой точки на ускорение g свободного падения в вакууме.
Вес тела – сумма модулей сил тяжести, действующих на частицы этого тела.
Внешняя сила – сила, действующая на какую-либо точку механической системы со стороны тел, не принадлежащих рассматриваемой механической системе.
Внутренние силы – силы, действующие на какие-либо точки механической системы со стороны других точек, принадлежащих рассматриваемой механической системе.
Система сил – любая совокупность сил, действующих на механическую систему.
Сосредоточенная сила – сила, приложенная к телу в какой-либо одной его точке.
Распределённые силы – силы, действующие на все точки некоторой части линии, поверхности или объёма.
Связи – материальные тела, накладывающие ограничения на положения и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах.
Реакции связей – силы, действующие на точки механической системы со стороны материальных тел, осуществляющих связи, наложенные на эту систему.
Инерциальная система отсчёта – система отсчета, по отношению к которой изолированная материальная точка находится в покое или движется равномерно и прямолинейно.
Естественные координатные оси – прямоугольная система осей с началом в движущейся точке, направленных соответственно по касательной, главной нормали и бинормали к траектории этой точки.
Восстанавливающая сила – сила, стремящаяся вернуть тело или точку в положение статического равновесия.
Амплитуда свободных колебаний – величина наибольшего отклонения точки от положения статического равновесия.
Период свободных колебаний – отрезок времени, за который точка проходит положение статического равновесия в одном и том же направлении.
Период затухающих колебаний – промежуток времени между двумя последовательными прохождениями точки в одном направлении через положение покоя.
Амплитуда затухающих колебаний – величина наибольшего отклонения точки в ту или другую сторону от положения статического равновесия в течение каждого колебания.
Сила инерции – величина, равная произведению массы материальной точки на её ускорение и направленная противоположно этому ускорению.
Переносная сила инерции при рассмотрении движения материальной точки в неинерциальной системе отсчёта – величина, равная произведению массы точки на её переносное ускорение и направленная противоположно этому ускорению.
Кориолисова сила инерции при рассмотрении движения точки в неинерциальной системе отсчёта – величина, равная произведению массы точки на её кориолисово ускорение и направленная противоположно этому ускорению.
Центр масс механической системы – геометрическая точка, для которой сумма произведений масс всех материальных точек, образующих механическую систему, на их радиус-векторы, проведенные из этой точки, равна нулю.
Момент инерции механической системы относительно оси – величина, равная сумме произведений масс всех материальных точек, образующих механическую систему, на квадраты их расстояний от данной оси.
Радиус инерции твердого тела относительно оси вращения – величина, произведение квадрата которой на массу тела равно моменту инерции тела относительно этой оси.
Радиус инерции механической системы относительно оси вращения – величина, квадрат которой равен отношению момента инерции механической системы относительно данной оси к массе этой системы.
Количество движения материальной точки – векторная мера механического движения, равная произведению массы точки на её скорость.
Элементарный импульс силы – векторная мера действия силы, равная произведению силы на элементарный промежуток времени её действия.
Импульс силы за конечный промежуток времени – величина, равная определенному интегралу от элементарного импульса силы, где пределами интеграла являются моменты начала и конца данного промежутка времени.
Количество движения механической системы – величина, равная сумме количеств движения всех материальных точек, образующих механическую систему.
Момент количества движения материальной точки относительно центра – величина, равная векторному произведению радиус-вектора материальной точки, проведенного из этого центра, на количество движения.
Момент количества движения точки относительно оси – величина, равная проекции на ось момента количества движения точки относительно любого выбранного на данной оси центра.
Момент количества движения m·V точки относительно оси – величина, равная алгебраической сумме моментов компонентов m·VOX, m·VOY, m·VOZ вектора m·V относительно этой оси.
Центральная сила – сила, линия действия которой постоянно проходит через некоторую точку, неподвижную в данной системе отсчета и называемую центром силы.
Кинетический момент или главный момент количеств движения механической системы относительно данного центра – величина, равная сумме моментов количеств движения всех точек механической системы относительно этого центра.
Кинетический момент или главный момент количеств движения механической системы относительно оси – величина, равная сумме моментов количеств движения всех точек механической системы относительно этой оси.
Элементарная работа силы – скалярная мера действия силы, равная скалярному произведению силы на элементарное перемещение точки её приложения.
Элементарное перемещение точки – перемещение точки из данного положения в положение, бесконечно близкое к нему.
Работа силы на конечном перемещении точки её приложения – величина, равная криволинейному интегралу от элементарной работы силы, действующей на данную материальную точку, взятому вдоль дуги кривой, описанной точкой при этом перемещении.
Мощность силы – величина, равная скалярному произведению силы на скорость точки её приложения.
Кинетическая энергия материальной точки – скалярная мера механического движения, равная половине произведения массы точки на квадрат её скорости движения.
Кинетическая энергия системы – величина, равная сумме кинетических энергий всех материальных точек механической системы.
Аналитическая механика – раздел механики, в котором изучается равновесие или движение механизмов с помощью общих, единых аналитических методов, применяемых для любых механических систем.
Обобщённые координаты механической системы – независимые между собой параметры, однозначно определяющие положение механической системы.
Возможное (виртуальное) перемещение точки – любое допускаемое наложенными связями перемещение материальной точки из положения, занимаемого ею в данный момент времени, в бесконечно близкое положение, которое она может занимать в тот же момент времени.
Мгновенный центр вращения – точка неподвижной плоскости, поворотом вокруг которой плоская фигура перемещается из данного положения в положение, бесконечно близкое к данному.
Уравнения связей – уравнения, которым в силу наложенных связей должны удовлетворять координаты точек механической системы и их скорости (первые производные от координат по времени).
Геометрические связи – связи, уравнения которых содержат только координаты точек механической системы.
Стационарные связи – связи, в уравнения которых время явно не входит.
Двусторнние (удерживающие) связи – связи, допускающие возможные перемещения только в двух взаимно противоположных направлениях.
Односторонние (неудерживающие) связи – связи, при которых точки механической системы имеют возможные перемещения, противоположные которым не являются возможными.
Возможное перемещение системы – любая совокупность возможных перемещений точек данной механической системы, допускаемая всеми наложенными на неё связями.
Возможная (элементарная) работа силы – бесконечно малая величина, равная скалярному произведению вектора силы F на вектор возможного перемещения δS точки её приложения.
Идеальные связи – связи, для которых сумма элементарных работ их реакций равна нулю на любом возможном перемещении механической системы.
Уравнения Лагранжа второго рода – дифференциальные уравнения движения механической системы в обобщённых координатах.
Обобщённая скорость – производная по времени от обобщённой координаты.
Обобщённая сила
Qqci по обобщенной координате
qci – величина, равная отношению
возможной элементарной работы δАS активных сил ![]() , приложенных к точкам механической системы, к
приращению δqci обобщенной координаты
qci.
, приложенных к точкам механической системы, к
приращению δqci обобщенной координаты
qci.
ВОПРОСЫ И ЗАДАНИЯ
ЭКЗАМЕНАЦИОННЫХ БИЛЕТОВ
1. Сформулировать первый закон динамики (закон инерции).
2. Сформулировать второй закон динамики (закон пропорциональности силы и ускорения).
3. Сформулировать третий закон динамики (закон равенства действия и противодействия).
4. Сформулировать четвёртый закон динамики (закон независимости действия сил).
5. Сформулировать определение понятия «инерциальная система отсчёта».
6. Записать основное уравнение динамики несвободной материальной точки в векторном виде.
7. Записать дифференциальные уравнения движения несвободной материальной точки в декартовой системе отсчёта.
8. Записать дифференциальные уравнения движения несвободной материальной точки в естественных координатных осях.
9. Сформулировать суть первой задачи динамики.
10. Сформулировать суть второй задачи динамики.
11. Как определяются постоянные интегрирования при решении второй задачи динамики?
12. Сформулировать определение понятия «восстанавливающая сила».
13. Сформулировать определение понятия «коэффициент жёсткости пружины».
14. Записать формулу для определения модуля силы упругости пружины.
15. Под действием каких сил осуществляются свободные колебания точки?
16. Записать дифференциальное уравнение свободных колебаний точки.
17. Записать уравнения свободных колебаний точки.
18. Сформулировать определение понятия «амплитуда свободных колебаний точки».
19. Сформулировать определение понятия «период свободных колебаний точки».
20. Сформулировать определение понятия «циклическая частота свободных колебаний точки».
21. Записать дифференциальное уравнение затухающих колебаний точки.
22. Записать уравнения затухающих колебаний точки.
23. Сформулировать определение понятия «период затухающих колебаний точки».
24. Сформулировать определение понятия «амплитуда затухающих колебаний точки».
25. Сформулировать определение понятия «циклическая частота затухающих колебаний».
26. Какие колебания называют колебаниями с малым сопротивлением внешней среды?
27. Записать уравнения апериодического движения точки.
28. Под действием каких сил происходят вынужденные колебания материальной точки?
29. Записать формулу для определения периода возмущающей силы.
30. Записать дифференциальное уравнение движения точки под действием восстанавливающей и возмущающей сил.
31. Записать уравнение вынужденных колебаний малой частоты.
32. Записать уравнение вынужденных колебаний большой частоты.
33. Записать условие, при котором происходит явление резонанса.
34. Записать дифференциальное уравнение движения точки, происходящее под действием восстанавливающей силы, возмущающей силы, изменяющейся по периодическому закону, и силы сопротивления движению, пропорциональной первой степени скорости.
35. Записать основное уравнение динамики относительного движения.
36. Записать формулу для определения переносной силы инерции.
37. Записать формулу для определения кориолисовой силы инерции.
38. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть неравномерное вращение относительно неподвижной оси, а относительное движение прямолинейное.
39. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть равномерное вращение относительно неподвижной оси, а относительное движение прямолинейное.
40. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть поступательное неравномерное криволинейное движение, а относительное движение прямолинейное.
41. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть прямолинейное и равномерное движение, а относительное движение прямолинейное.
42. Сформулировать принцип относительности классической механики.
43. Сформулировать определение понятия «механическая система».
44. Сформулировать определение понятия «свободная механическая система».
45. Сформулировать определение понятия «несвободная механическая система».
46. Сформулировать определение понятия «внешние силы».
47. Сформулировать определение понятия «внутренние силы».
48. Сформулировать определение понятия «неизменяемая механическая система».
49. Сформулировать определение понятия «центр масс механической системы».
50. Записать формулу для определения радиус-вектора центра масс механической системы.
51. Записать формулу для определения главного вектора активных сил.
52. Записать формулу для определения главного вектора реакций внешних связей.
53. Записать формулу для определения главного вектора реакций внутренних связей.
54. Записать формулу для определения вектора скорости центра масс механической системы.
55. Записать формулу для определения вектора ускорения центра масс механической системы.
56. Записать формулы для определения проекций вектора скорости центра масс механической системы на координатные оси.
57. Записать формулы для определения проекций вектора ускорения центра масс механической системы на координатные оси.
58. Записать формулу для определения модуля скорости центра масс механической системы.
59. Записать формулу для определения модуля ускорения центра масс механической системы.
60. Что является мерой инертности при поступательном движении твёрдого тела?
61. Что является мерой инертности при вращательном движении твёрдого тела?
62. Сформулировать определение понятия «момент инерции тела относительно оси вращения».
63. Что характеризует момент инерции тела относительно оси вращения?
64. Сформулировать теорему Штейнера.
65. Записать формулу для определения момента инерции тела относительно вертикальной оси вращения.
66. Сформулировать определение «радиус инерции твёрдого тела относительно оси вращения».
67. Записать формулу для определения момента инерции механической системы.
68. Сформулировать теорему о движении центра масс механической системы.
69. Записать векторную формулу, выражающую теорему о движении центра масс механической системы.
70. Записать дифференциальные уравнения движения центра масс механической системы в декартовой системе отсчёта.
71. Сформулировать первое следствие из теоремы о движении центра масс механической системы.
72. Сформулировать второе следствие из теоремы о движении центра масс механической системы.
73. Сформулировать определение понятия «количество движения материальной точки».
74. Сформулировать определение понятия «импульс силы за промежуток времени».
75. Записать формулу для определения импульса силы за промежуток времени.
76. Сформулировать определение понятия «количество движения механической системы».
77. Записать теорему об изменении количества движения механической системы в векторной форме.
78. Записать теорему об изменении количества движения механической системы в скалярной форме.
79. Сформулировать определение понятия «момент количества движения точки относительно произвольного центра».
80. Сформулировать определение понятия «плечо вектора количества движения точки относительно произвольного центра».
81. Сформулировать определение понятия «момент количества движения точки относительно оси».
82. Записать формулы для определения моментов количества движения точки относительно координатных осей.
83. Записать в векторной форме формулу, выражающую теорему об изменении момента количества движения материальной точки.
84. Записать в скалярном виде формулу, выражающую теорему об изменении момента количества движения материальной точки.
85. Сформулировать определение понятия «центральная сила».
86. Сформулировать определение понятия «кинетический момент механической системы относительно оси».
87. Записать в скалярном виде формулу, выражающую теорему об изменении кинетического момента механической системы относительно координатных осей.
88. Сформулировать следствия из теоремы об изменении кинетического момента механической системы относительно координатных осей.
89. Записать дифференциальные уравнения поступательного движения твёрдого тела в пространстве.
90. Записать дифференциальное уравнение вращательного движения твёрдого тела относительно вертикальной оси.
91. Записать дифференциальные уравнения плоскопараллельного движения твёрдого тела.
92. Сформулировать определение понятия «работа постоянной силы на прямолинейном перемещении точки её приложения».
93. Сформулировать определение понятия «элементарная работа переменной силы».
94. Записать формулу для определения работы силы тяжести.
95. Сформулировать определение понятия «мощность силы».
96. Сформулировать определение понятия «кинетическая энергия».
97. Записать формулу для определения кинетической энергии материальной точки.
98. Записать формулу для определения кинетической энергии поступательно движущегося твёрдого тела.
99. Записать формулу для определения кинетической энергии вращающегося тела относительно вертикальной оси.
100. Записать формулу для определения кинетической энергии для твёрдого тела, совершающего плоскопараллельное движение.
101. Записать формулу для определения кинетической энергии механической системы.
102. Записать формулу, выражающую теорему об изменении кинетической энергии механической системы.
103. Сформулировать определение понятия «сила инерции».
104. Записать формулу для определения силы инерции материальной точки.
105. Записать формулу, выражающую принцип Даламбера для несвободной материальной точки в векторной форме.
106. Записать формулы, выражающие принцип Даламбера для несвободной материальной точки в координатной форме.
107. Записать формулы, выражающие принцип Даламбера для несвободной механической системы в векторной форме.
108. Записать формулы, выражающие принцип Даламбера для несвободной неизменяемой механической системы в координатной форме.
109. Записать формулу для определения главного вектора сил инерции поступательно движущегося твёрдого тела.
110. Записать формулы, по которым определяются центробежная и вращательная силы инерции и момент сил инерции при вращательном движении тела относительно оси, не проходящей через центр масс, в случае, когда силы инерции приложены в центре масс.
111. Записать формулу для определения момента сил инерции при вращении тела относительно оси, проходящей через его центр масс.
112. Записать формулы для определения инерционных нагрузок при плоскопараллельном движении твёрдого тела.
113. Сформулировать определение понятия «обобщённые координаты механической системы».
114. Что изучает аналитическая механика?
115. Сформулировать определение понятия «возможные перемещения несвободной механической системы».
116. Сформулировать определение понятия «связи».
117. Сформулировать определение понятия «геометрические связи».
118. Сформулировать определение понятия «стационарные связи».
119. Сформулировать определение понятия «уравнения связей».
120. Сформулировать определение понятия «двусторонние (удерживающие) связи».
121. Сформулировать определение понятия «односторонние (неудерживающие) связи».
122. Сформулировать определение понятия «возможное перемещение системы».
123. Сформулировать определение понятия «возможная (элементарная) работа силы».
124. Записать формулу для определения возможной работы силы.
125. Записать формулу для определения возможной работы сил, приложенных к механической системе.
126. Сформулировать определение понятия «идеальные связи».
127. Сформулировать принцип возможных перемещений.
128. Записать формулу, выражающую принцип возможных перемещений в векторной форме.
129. Записать формулу, выражающую принцип возможных перемещений в координатной форме.
130. Записать формулу, выражающую принцип возможных скоростей (принцип возможных мощностей).
131. Сформулировать общее уравнение динамики.
132. Записать формулу, выражающую общее уравнение динамики в векторной форме.
133. Записать формулу, выражающую общее уравнение динамики в скалярной форме.
134. Записать формулу, выражающую общее уравнение динамики, в координатной форме.
135. Записать уравнение Лагранжа второго рода.
136. Сформулировать определение понятия «обобщённая сила».
ВАРИАНТ
ЭКЗАМЕНАЦИОННЫХ БИЛЕТОВ
Порядок
выбора экзаменационного билета
Экзаменационные билеты содержат теоретические и практические задания по разделу «Динамика» курса теоретической механики.
Теоретическая часть экзаменационного билета сформирована из вопросов и заданий для самоконтроля, приведённых в учебно-методическом пособии А. М. Лукина, В. В. Квалдыкова «Теоретическая механика (раздел «Динамика»)»: – Омск: СибАДИ, 2010. – 344 с.).). Эта часть экзаменационного билета содержит десять заданий.
Практическая часть экзаменационного билета состоит из пяти заданий и содержит некоторые вопросы, решаемые студентами при выполнении расчётно-графических работ.
Экзаменационный билет студент выбирает самостоятельно по двум последним цифрам номера своей зачётной книжки, используя следующую формулу:
b = c – 30·i,
где b – номер экзаменационного билета; с – две последние цифры номера зачётной книжки студента; 30 – число предложенных студенту экзаменационных билетов; i – целое число, изменяющееся от 0 до 3.
Примеры определения номера экзаменационного билета:
с = 06, b = 06 - 30·0 = 6. Билет №6.
с = 32, b = 32 - 30·1 = 2. Билет №2.
с = 73, b = 73 - 30·2 = 13. Билет №13.
с = 95, b = 95 - 30·3 = 5. Билет №15.
Ответы на экзаменационный билет студент высылает на адрес СибАДИ.
Пример ответа на экзаменационный билет
Теоретическая часть
Задание 1. Сформулировать второй закон динамики.
Ответ. Второй закон динамики – ускорение материальной точки пропорционально приложенной к ней силе, имеет одинаковое с ней направление.
Задание 2. Сформулировать определение термина «инерциальная система отсчёта».
Ответ. Инерциальная система отсчёта – система отсчёта, по отношению к которой изолированная материальная точка находится в покое или движется равномерно и прямолинейно.
Задание 3. Сформулировать содержание второй задачи динамики.
Ответ. Содержание второй задачи динамики – зная силы, действующие на точку, её массу, а также начальное положение точки и её начальную скорость, требуется определить уравнения движения точки.
Задание 4. Записать дифференциальные уравнения движения несвободной материальной точки в декартовой системе отсчёта.
Ответ. Дифференциальные уравнения движения несвободной материальной точки в декартовой системе отсчёта:
m·![]() = ∑
= ∑![]() + ∑
+ ∑![]() ; m·
; m·![]() = ∑
= ∑![]() + ∑
+ ∑![]() ;
;
m·![]() = ∑
= ∑![]() + ∑
+ ∑![]() ,
,
где
m –
масса точки; ![]() ,
, ![]() ,
, ![]() – проекции ускорения точки на координатные
оси; ∑
– проекции ускорения точки на координатные
оси; ∑![]() , ∑
, ∑![]() , ∑
, ∑![]() – суммы проекций активных
сил на соответствующие координатные оси; ∑
– суммы проекций активных
сил на соответствующие координатные оси; ∑![]() , ∑
, ∑![]() , ∑
, ∑![]() – суммы проекций реакций внешних связей на
координатные оси.
– суммы проекций реакций внешних связей на
координатные оси.
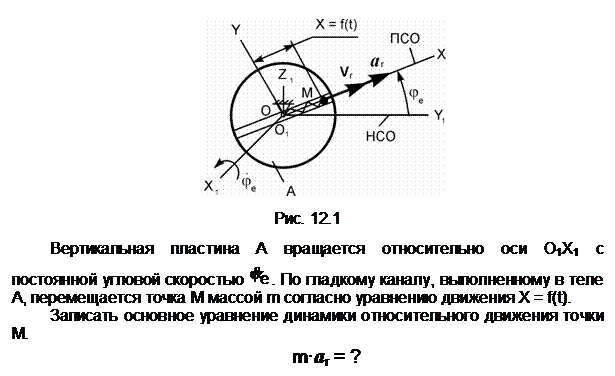
Задание 5. Записать основное уравнение динамики относительного движения точки.
Ответ. Основное уравнение динамики относительного движения точки имеет вид
m·ar = ∑FiЕ + ∑RiЕ + Фе + Фс,
где m – масса точки; ar – относительное ускорение точки; ∑FiЕ – геометрическая сумма активных сил; ∑RiЕ – геометрическая сумма реакций внешних связей; Фе – переносная сила инерции; Фс – кориолисова сила инерции.
Задание 6. Что является мерой инертности при вращательном движении твёрдого тела?
Ответ. Мерой инертности твёрдого тела при его вращательном движении является момент инерции тела относительно оси вращения.
Задание 7. Записать дифференциальное уравнение вращательного движения твёрдого тела относительно оси ОХ.
Ответ. Дифференциальное уравнение вращательного движения твердого тела относительно оси ОХ имеет вид
JOX·![]() = ∑MOX(
= ∑MOX(![]() + ∑MOX(
+ ∑MOX(![]() ),
),
где
JOX
–
момент инерции тела относительно оси вращения ОХ; ![]() – угловое ускорение тела; ∑MOX(
– угловое ускорение тела; ∑MOX(![]() –
сумма моментов активных сил относительно оси вращения; ∑MOX(
–
сумма моментов активных сил относительно оси вращения; ∑MOX(![]() ) – сумма моментов реакций внешних связей относительно оси
вращения.
) – сумма моментов реакций внешних связей относительно оси
вращения.
Задание 8. Записать формулу для определения кинетической энергии твёрдого тела при его поступательном движении.
Ответ. Кинетическую энергию твёрдого тела при его поступательном движении определяют по формуле
T = m·(VС)2/2,
где Т – кинетическая энергия; m – масса тела; VС – скорость центра масс твёрдого тела.
Задание 9. Сформулировать определение понятия «обобщённые координаты механической системы».
Ответ. Обобщенные координаты механической системы – независимые величины, заданием которых однозначно определяются положения точек механической системы.
Задание 10. Сформулировать определение понятия «механическая система».
Ответ. Механическая система – любая совокупность материальных точек, движения которых взаимозависимы.
Практическая часть

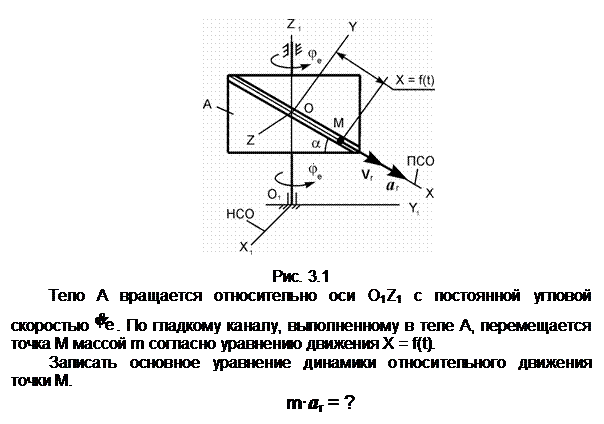
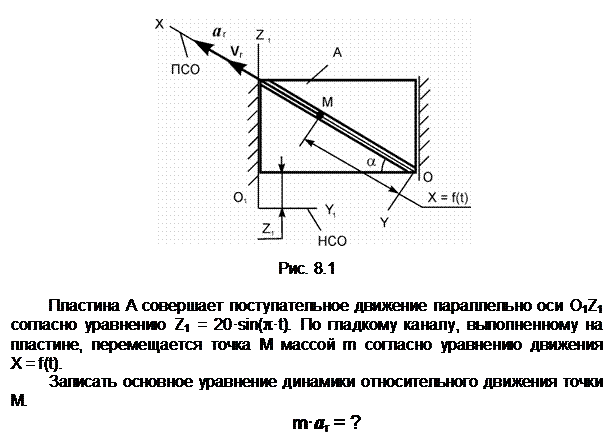
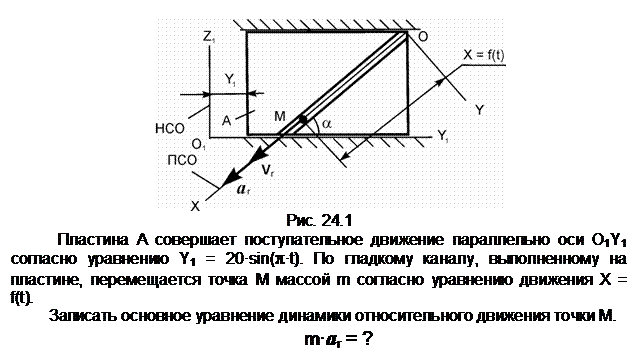
Задание 1

Решение
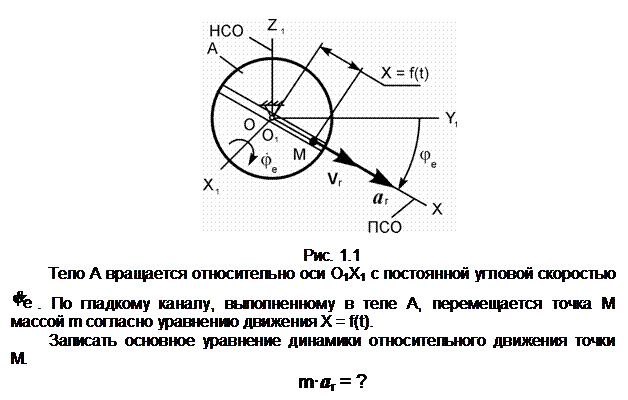
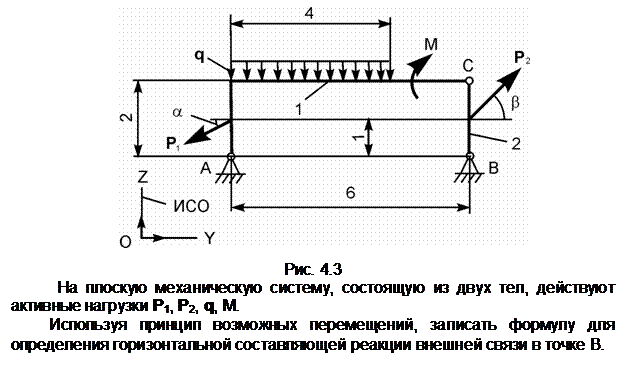
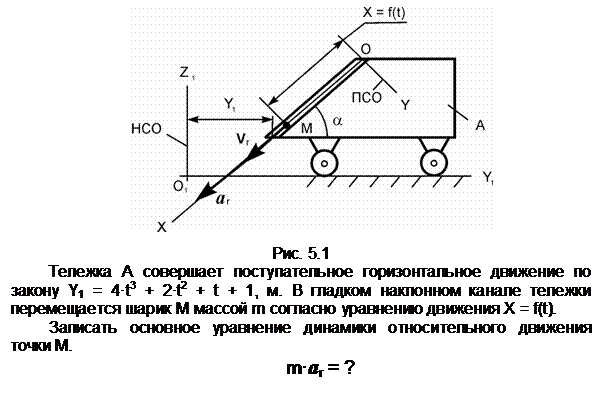
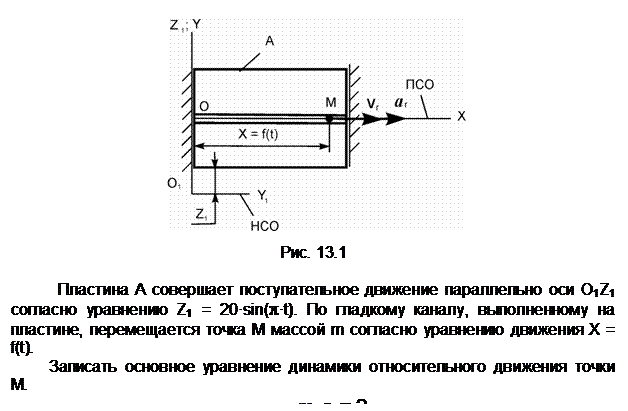
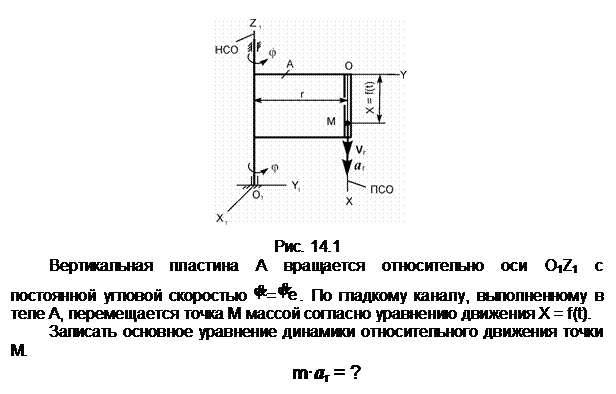
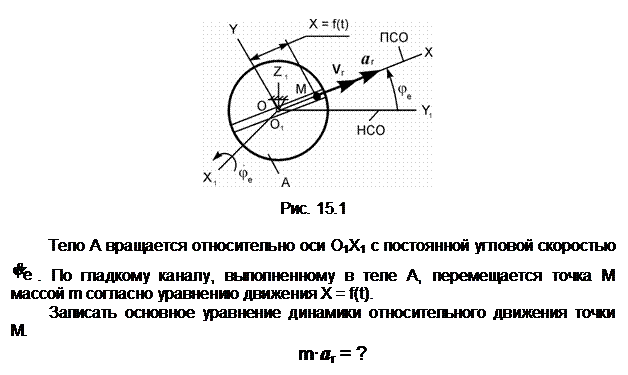
Пояснения к решению
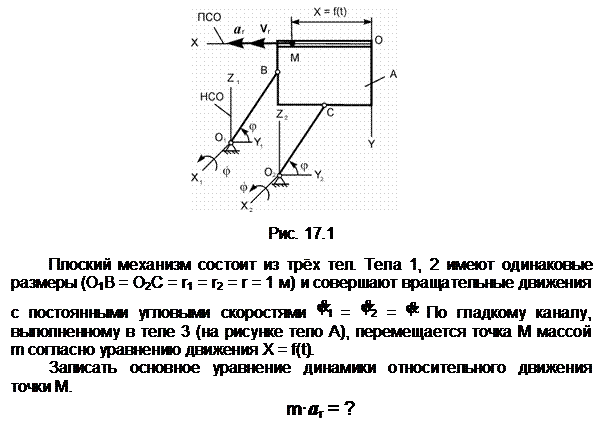
aA – ускорение точки А тела 1,
совершающего вращательное движение; aA
= ![]() ·r
=
·r
= ![]() ·r – модуль
ускорения точки А тела 1;. aе – переносное ускорение; aе =
aA; ar – относительное ускорение. Vr – относительная скорость.
G – сила тяжести.
N – нормальная реакция. Фе
– переносная сила инерции. Х =
f(t) – уравнение относительного
движения точки.
·r – модуль
ускорения точки А тела 1;. aе – переносное ускорение; aе =
aA; ar – относительное ускорение. Vr – относительная скорость.
G – сила тяжести.
N – нормальная реакция. Фе
– переносная сила инерции. Х =
f(t) – уравнение относительного
движения точки.
Фе =
m·ae =
m·![]() ·r.
·r.
Ответ: m·ar = G + N + Фе.
Задание 2
Решение

Пояснения к решению
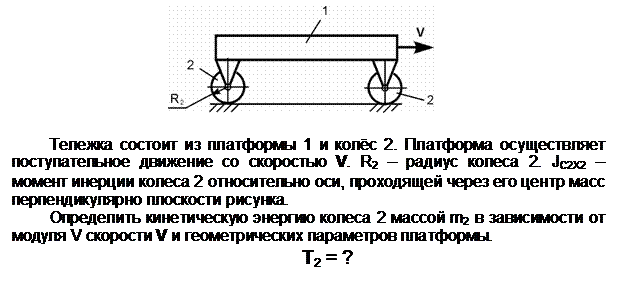
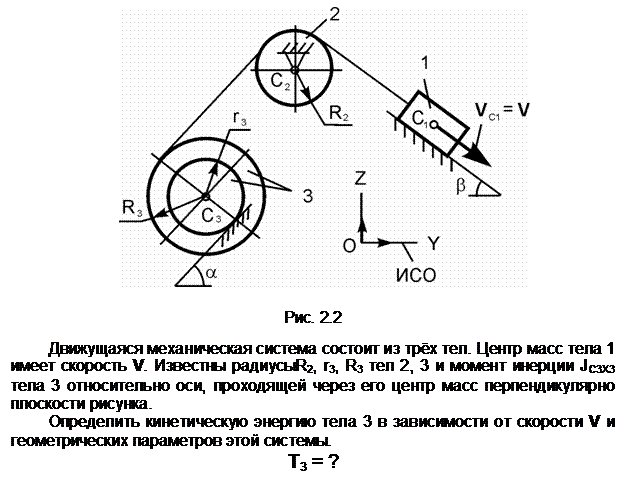
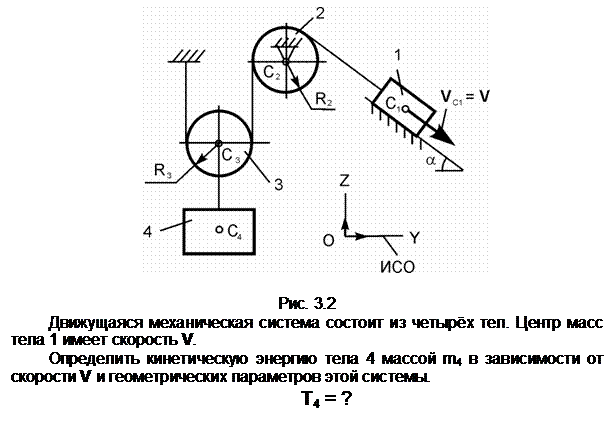
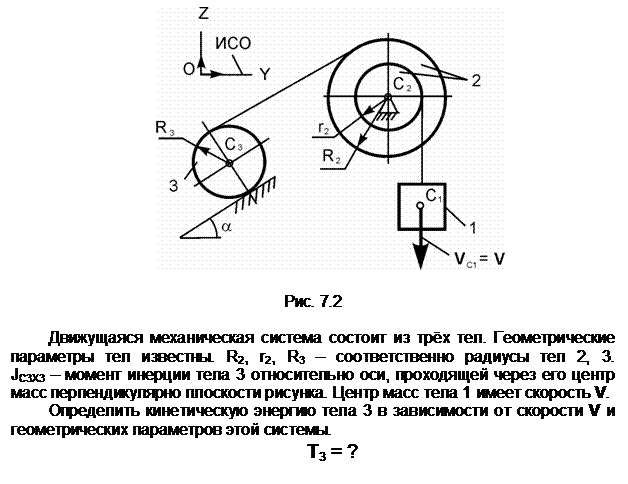
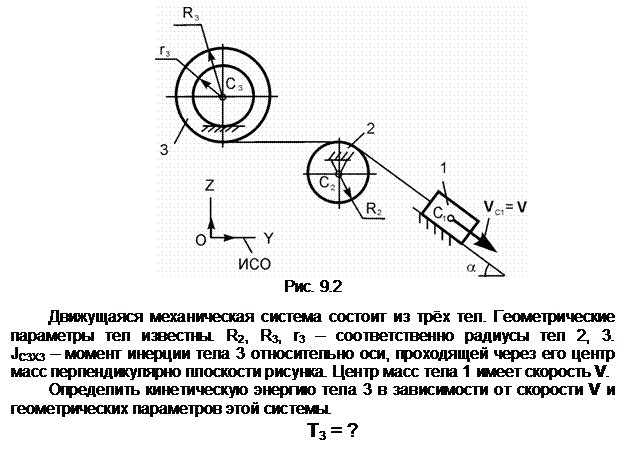
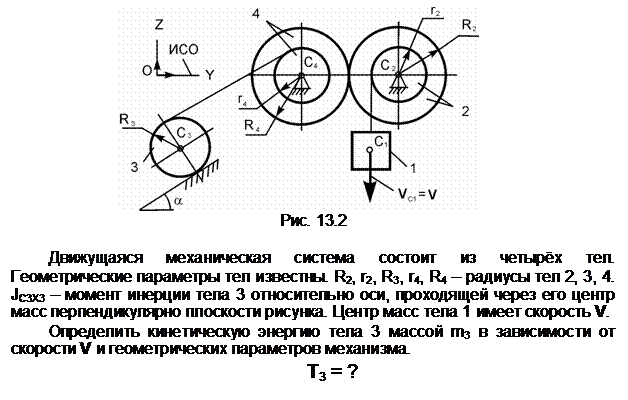
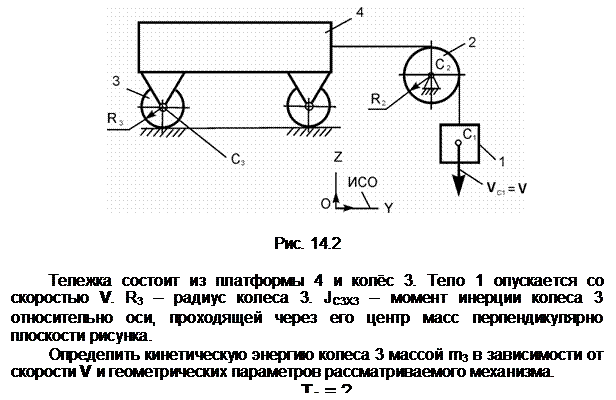
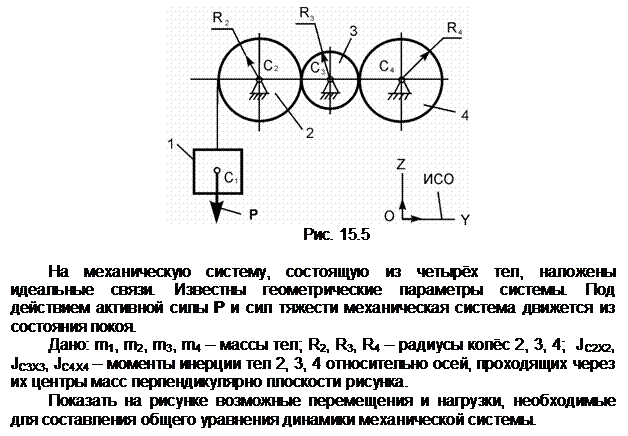
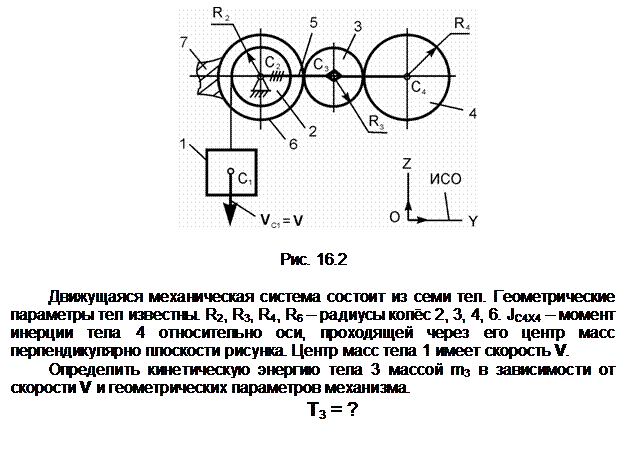
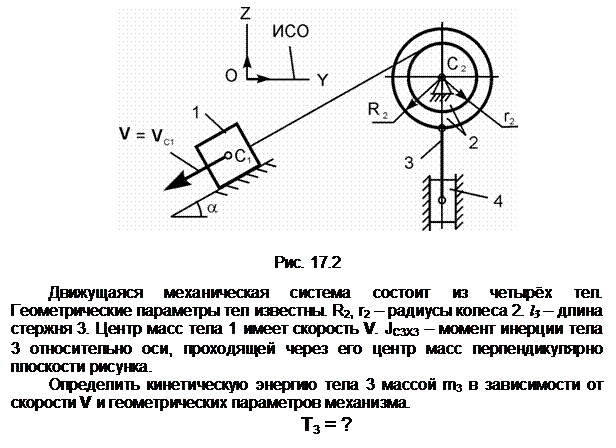
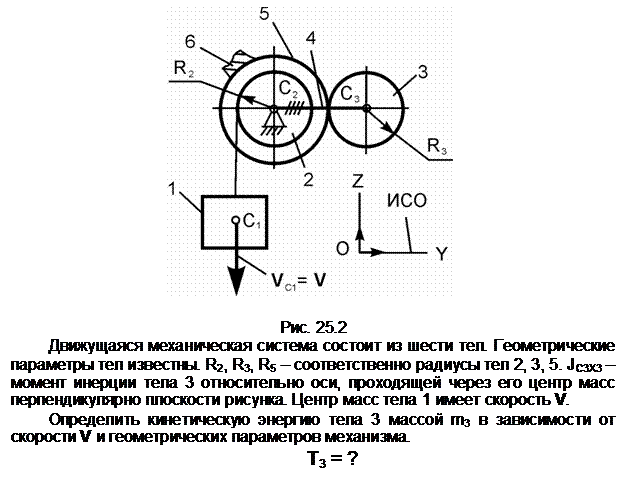
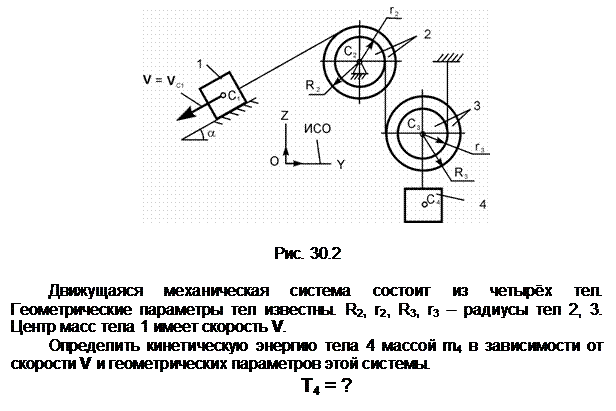
Тело 2 осуществляет плоскопараллельное движение. Его кинетическую энергию определяют по формуле
Т2 =
m2·(VC2)2/2 +
JC2X2·![]() /2,
/2,
где
m2 – масса тела 2;
VC2 – скорость центра С2
масс тела 2; VC2 = V;
JC2X2 – момент
инерции тела относительно оси С2Х2, проходящей через его
центр масс перпендикулярно плоскости рисунка; ![]() – угловая скорость тела 2; точка Р2
– мгновенный центр скоростей тела 2.
– угловая скорость тела 2; точка Р2
– мгновенный центр скоростей тела 2.
![]() =
VC2/R2 = V/R2.
=
VC2/R2 = V/R2.
Ответ: T2 = (m2·V2)/2 + (JС2Х2·(V/R2)2)/2.
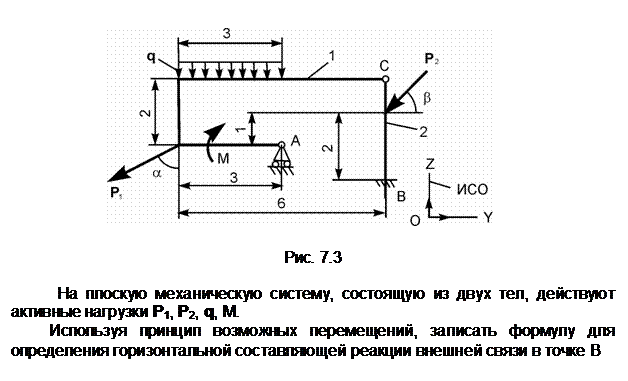
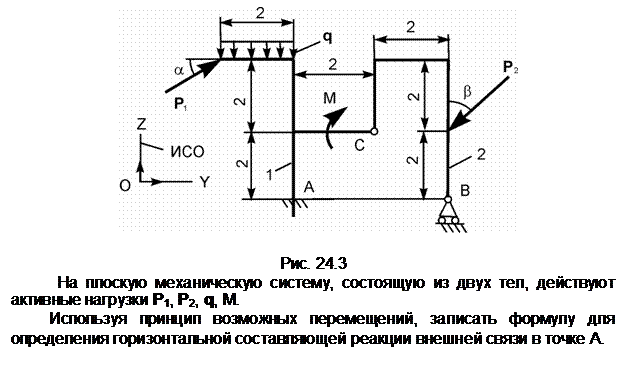
Задание 3
Решение

Пояснения к решению
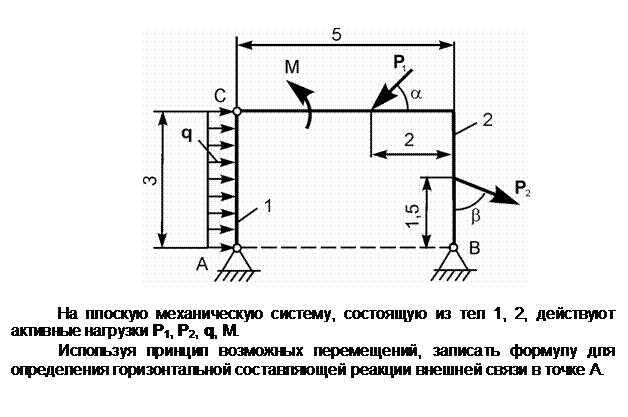
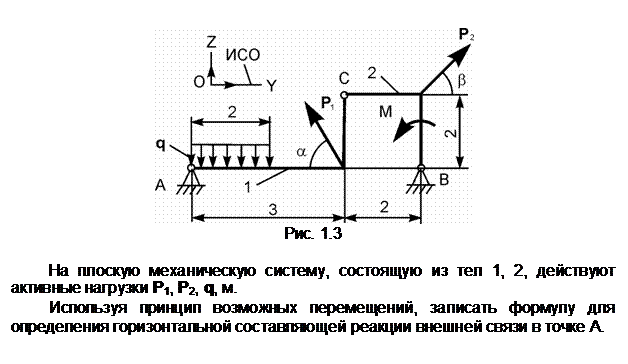
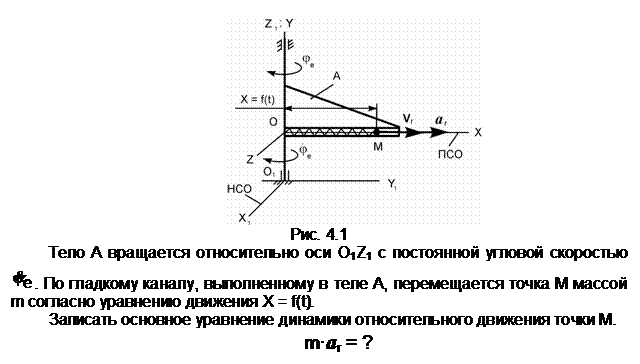
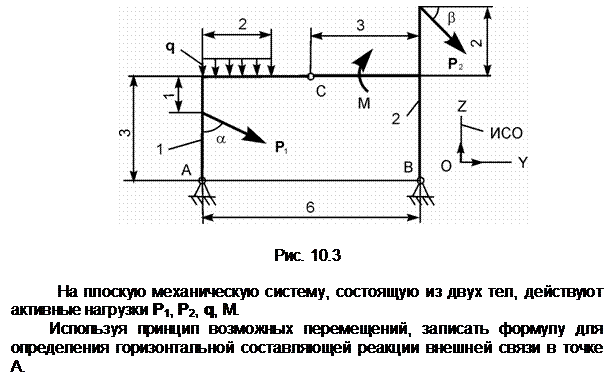
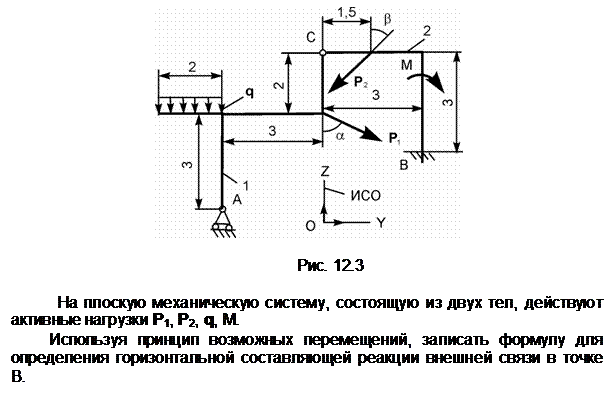
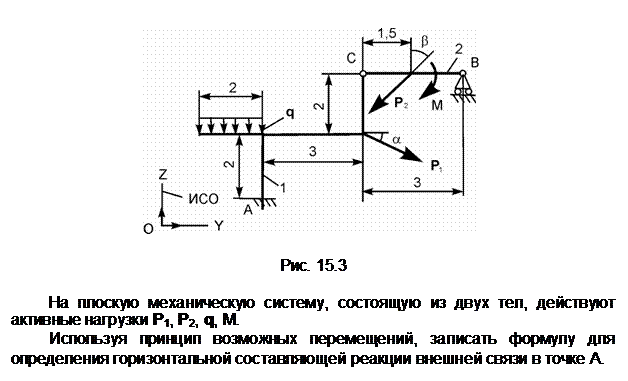
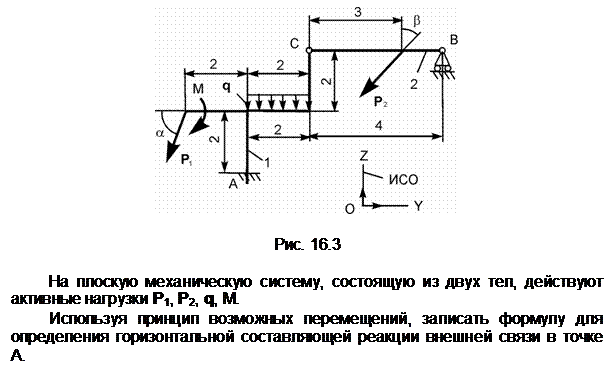
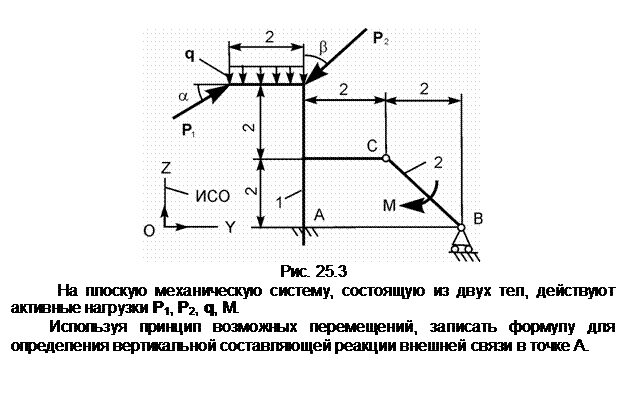
Распределённую нагрузку заменим сосредоточенной силой Q.
Снимем связь по горизонтали и перенесём реакцию ХА в разряд активных сил. Зададим возможное перемещение dSA точке А тела 1. S1 – мгновенный центр поворота тела 1; dj1 – возможное угловое перемещение тела 1; Точка приложения силы Q получит возможное перемещение dSQ = dSA/2.
Ответ: Q· dSQ + XA· dSA = 0.
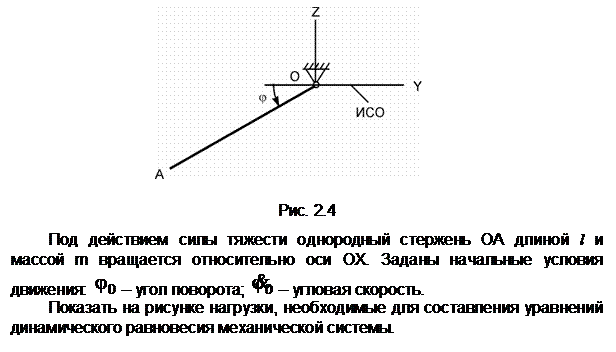
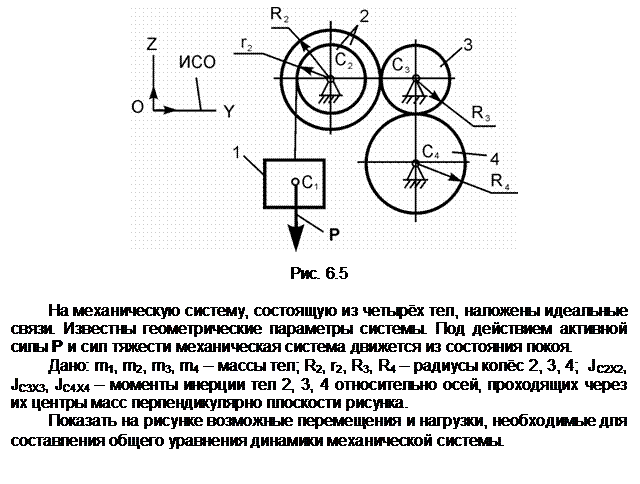
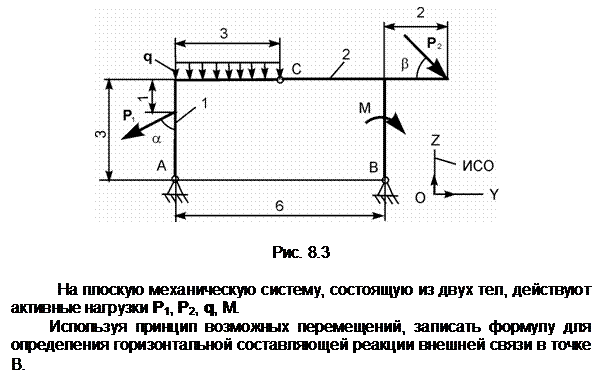
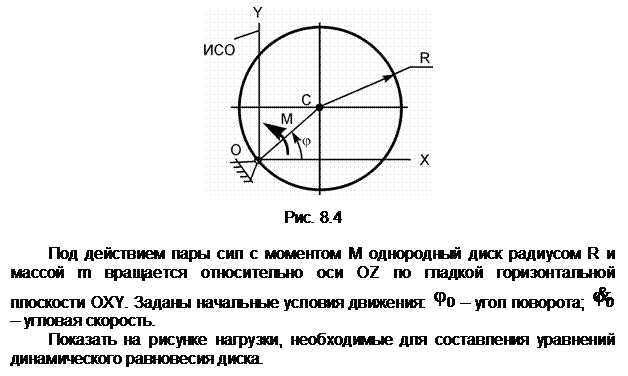
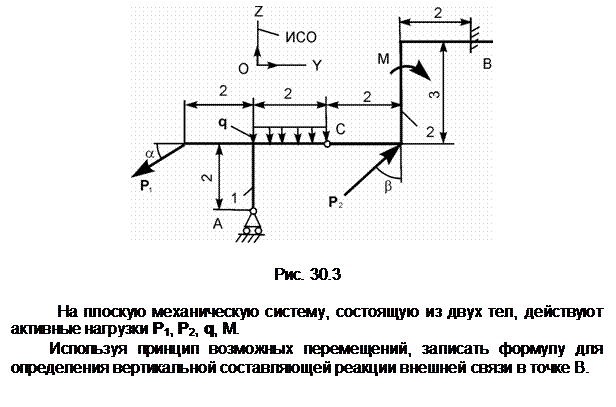
Задание 4
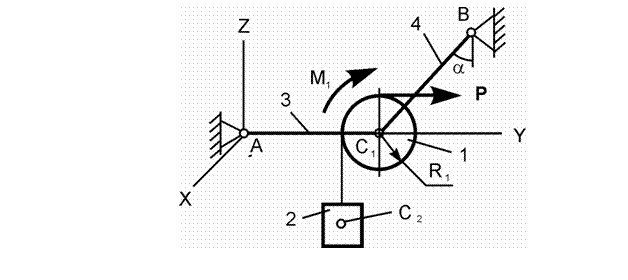
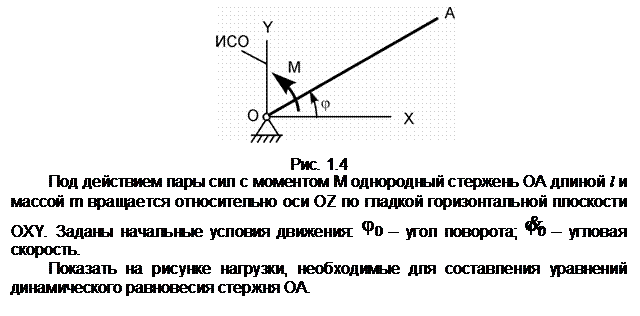
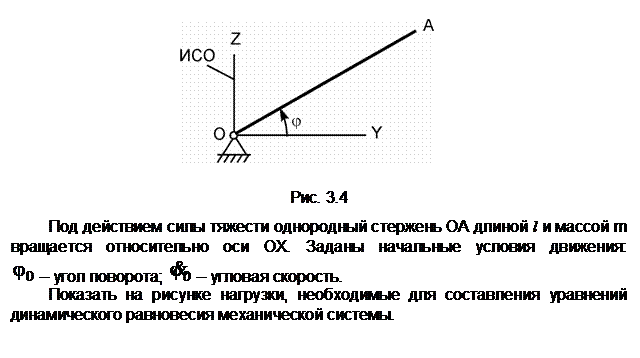
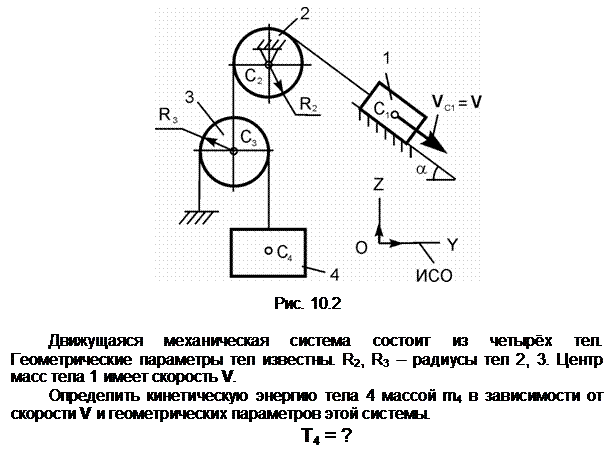
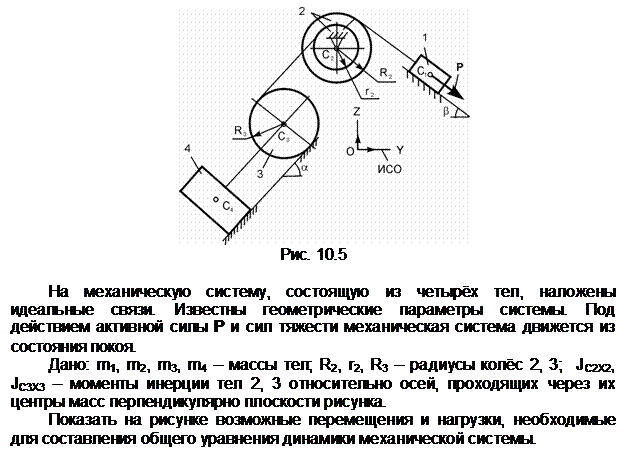
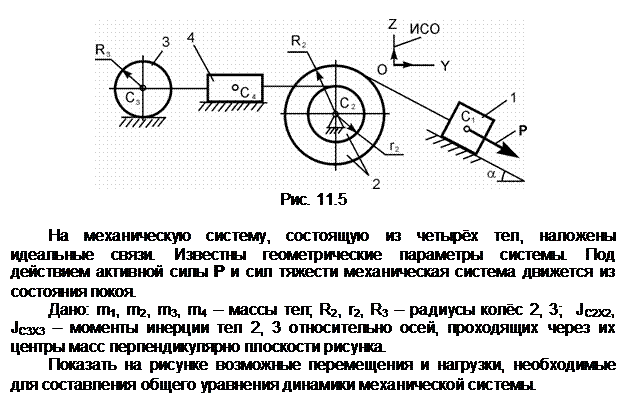
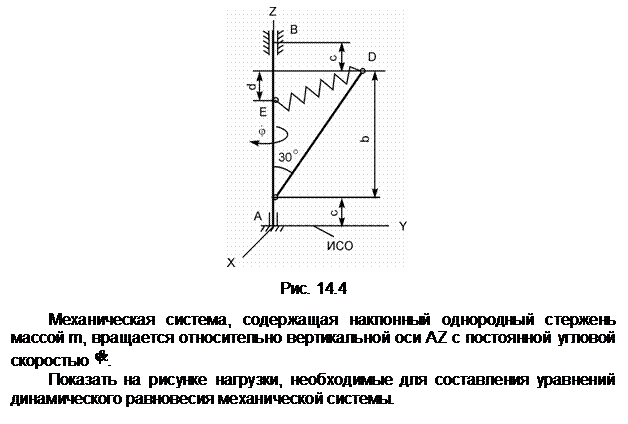
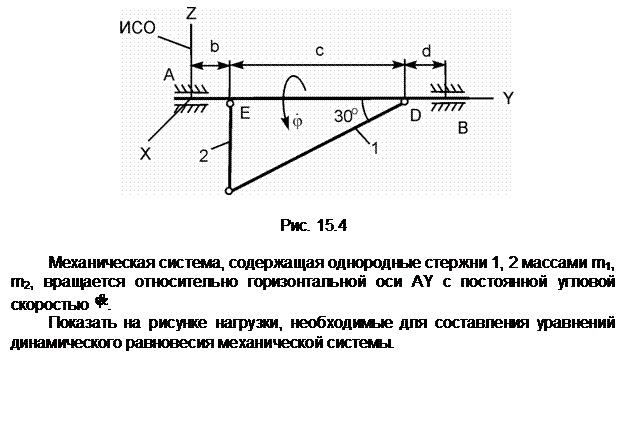
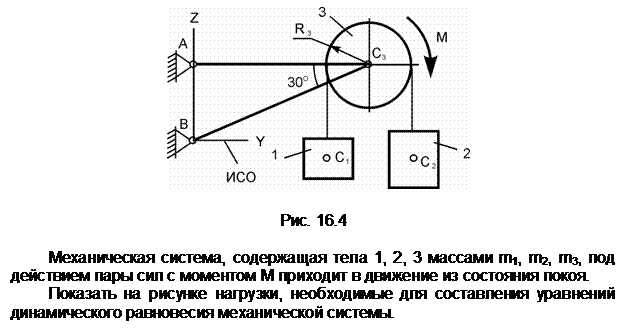
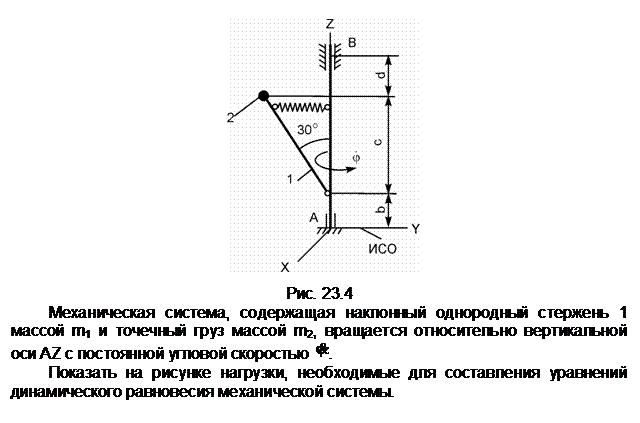
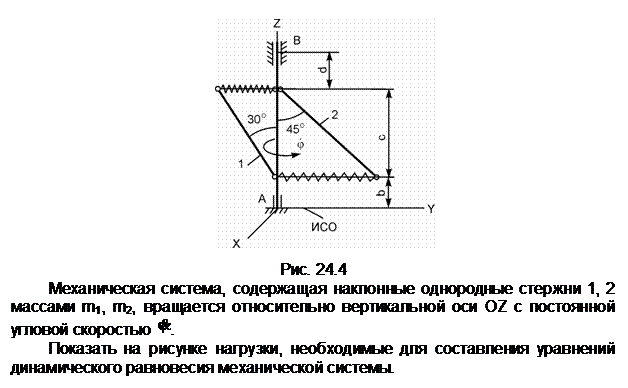
Механическая система, состоящая из однородного диска 1 с массой m1, груза 2 массой m2, невесомых стержней 3, 4 и нити, приходит в движение из состояния покоя. Р – активная сила; М1 – активный момент; R1 – радиус тела 1; JС1Х1 – радиус инерции тела 1 относительно оси, проходящей через его центр масс перпендикулярно плоскости рисунка.
Показать на рисунке нагрузки, необходимые для составления уравнений динамического равновесия механической системы, состоящей из тел 1 – 4.
Решение

Пояснения к решению
Обозначения на рисунке:
G1 – сила тяжести диска 1;
G2 – сила тяжести груза 2; С1,
С2 – соответственно центры масс тел 1 и 2; aC2 – ускорение центра масс груза 2; ![]() - угловое ускорение диска 1; Ф2 –
сила инерции груза 2;
- угловое ускорение диска 1; Ф2 –
сила инерции груза 2; ![]() –
приведённый момент сил инерции диска 1;
RA,
RB – реакции связей в точках А и В.
–
приведённый момент сил инерции диска 1;
RA,
RB – реакции связей в точках А и В.
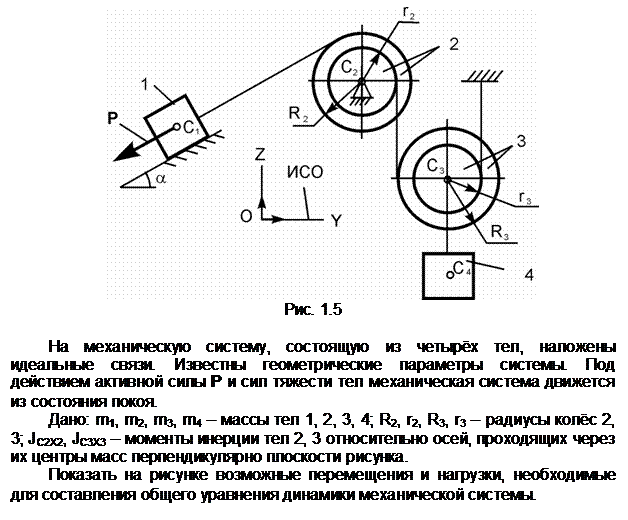
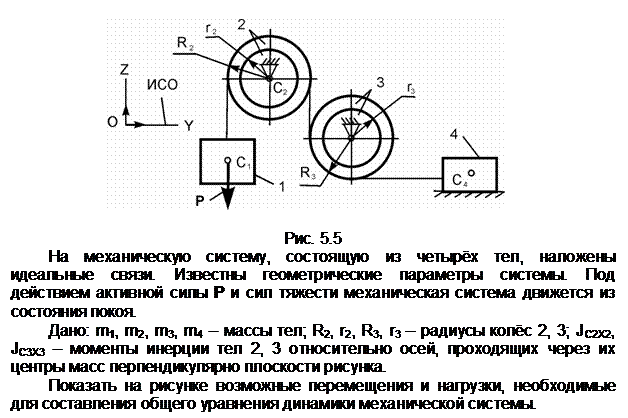
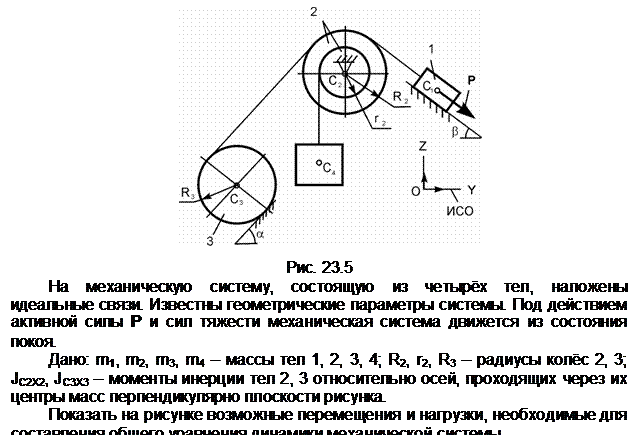
Задание 5
Решение
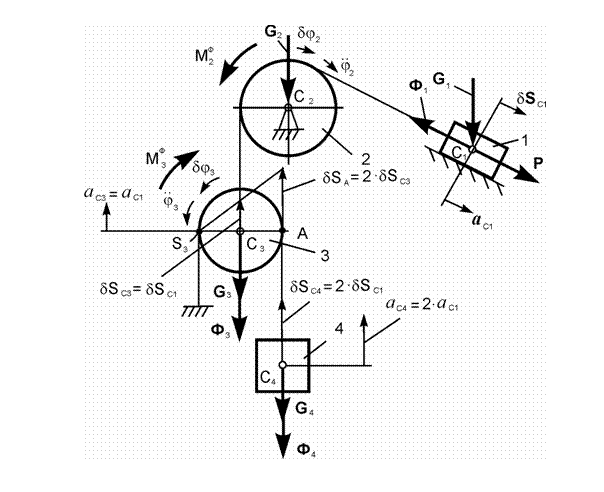
Пояснения к решению
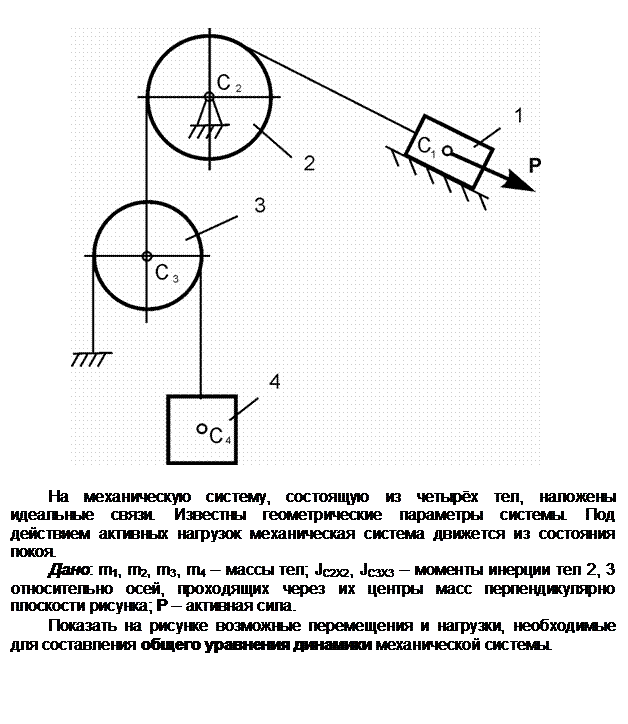
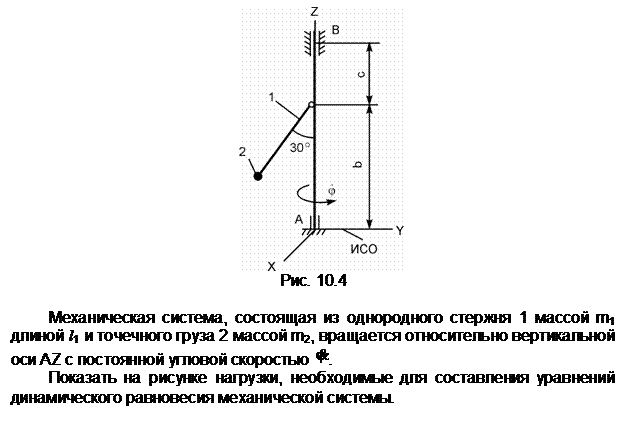
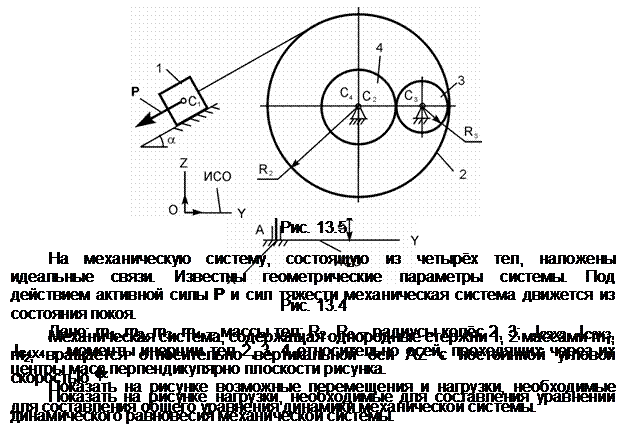
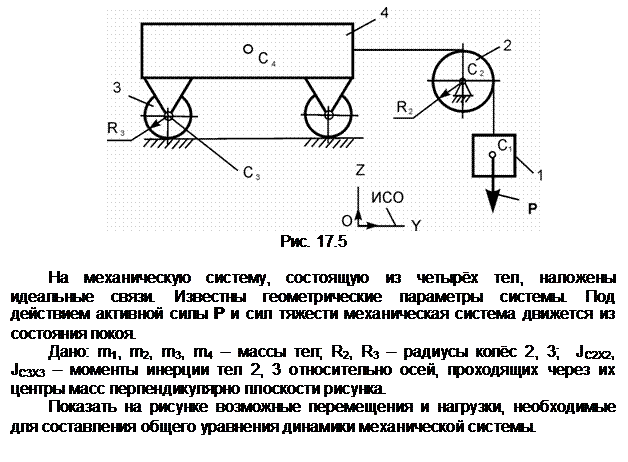
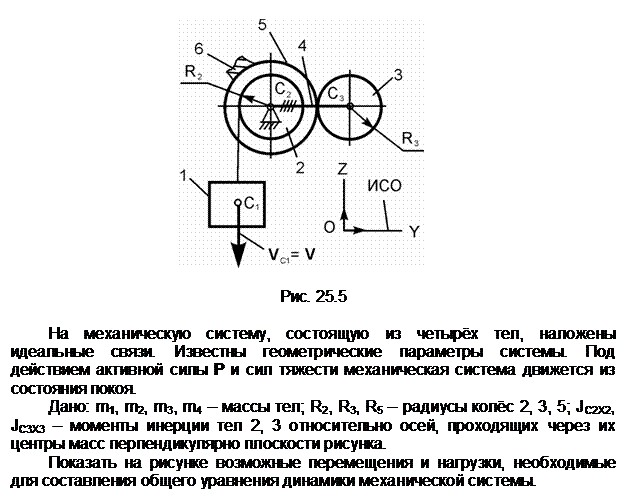
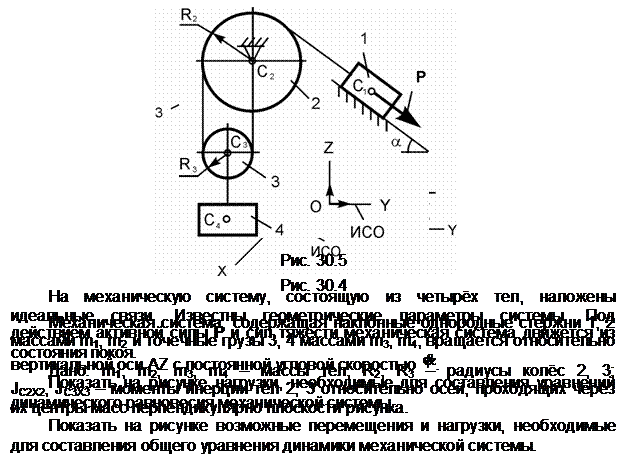
Обозначения на рисунке:
G1,
G2,
G3,
G4 – силы тяжестей тел 1, 2, 3, 4; Ф1,
Ф3, Ф4 – силы инерции тел 1, 3, 4; ![]() ,
, ![]() – приведённые моменты сил инерции
тел 2, 3; dSC1, dSC3 ,
dSC4, – возможное перемещение центров
масс тел 1, 3, 4; dj2, dj3 - возможные угловые перемещения тел 2, 3;
– приведённые моменты сил инерции
тел 2, 3; dSC1, dSC3 ,
dSC4, – возможное перемещение центров
масс тел 1, 3, 4; dj2, dj3 - возможные угловые перемещения тел 2, 3; ![]() - угловые ускорения тел 2, 3;
aC1 – ускорение центра масс тела 1;
aC1, aC3, aC4 – модули ускорений центров масс тел
1, 3, 4.
- угловые ускорения тел 2, 3;
aC1 – ускорение центра масс тела 1;
aC1, aC3, aC4 – модули ускорений центров масс тел
1, 3, 4.
ЭКЗАМЕНАЦИОННЫЕ БИЛЕТЫ
Билет № 1
Теоретическая часть
Задание 1. Сформулировать второй закон динамики (закон пропорциональности силы и ускорения).
Задание 2. Сформулировать определение понятия «период свободных колебаний точки».
Задание 3. Записать формулу для определения периода возмущающей силы.
Задание 4. Сформулировать определение понятия «механическая система».
Задание 5. Что является мерой инертности при вращательном движении твёрдого тела?
Задание 6. Сформулировать определение понятия «количество движения материальной точки».
Задание 7. Записать формулу для определения кинетической энергии поступательно движущегося твёрдого тела.
Задание 8. Записать формулу для определения момента сил инерции при вращении тела относительно оси, проходящей через его центр масс.
Задание 9. Сформулировать общее уравнение динамики.
Задание 10. Записать формулу, выражающую общее уравнение динамики, в скалярной форме.
Практическая часть
Задание 1
Задание 2

Задание 3
Задание 4
Задание 5
Билет № 2
Теоретическая часть
Задание 1. Сформулировать третий закон динамики (закон равенства действия и противодействия).
Задание 2. Записать уравнения апериодического движения точки.
Задание 3. Записать формулу для определения переносной силы инерции.
Задание 4. Записать формулу для определения вектора ускорения центра масс механической системы.
Задание 5. Сформулировать второе следствие из теоремы о движении центра масс механической системы.
Задание 6. Сформулировать определение понятия «момент количества движения точки относительно оси».
Задание 7. Записать формулу для определения главного вектора сил инерции поступательно движущегося твёрдого тела.
Задание 8. Записать теорему об изменении количества движения механической системы в векторной форме.
Задание 9. Записать дифференциальные уравнения поступательного движения твёрдого тела в пространстве.
Задание 10. Сформулировать первый закон динамики (закон инерции).
Практическая часть

Задание 1
Задание 2
Задание 3

Задание 4

Задание 5
Билет № 3
Теоретическая часть
Задание 1. Сформулировать третий закон динамики (закон равенства действия и противодействия).
Задание 2. Под действием каких сил происходят вынужденные колебания материальной точки?
Задание 3. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть поступательное неравномерное криволинейное движение, а относительное движение прямолинейное.
Задание 4. Что является мерой инертности при поступательном движении твёрдого тела?
Задание 5. Сформулировать второе следствие из теоремы о движении центра масс механической системы.
Задание 6. Сформулировать определение понятия «центральная сила».
Задание 7. Сформулировать определение понятия «кинетическая энергия».
Задание 8. Сформулировать определение понятия «возможные перемещения несвободной механической системы».
Задание 9. Что изучает аналитическая механика?
Задание 10. Сформулировать определение понятия «обобщённая сила».
Практическая часть
Задание 1
Задание 2

Задание 3
Задание 4
Задание 5

Билет № 4
Теоретическая часть
Задание 1. Сформулировать определение понятия «инерциальная система отсчёта».
Задание 2. Под действием каких сил происходят вынужденные колебания материальной точки?
Задание 3. Записать дифференциальное уравнение движения точки, происходящее под действием восстанавливающей силы, возмущающей силы, изменяющейся по периодическому закону, и силы сопротивления движению, пропорциональной первой степени скорости.
Задание 4. Что является мерой инертности при поступательном движении твёрдого тела?
Задание 5. Записать формулу для определения момента инерции тела относительно вертикальной оси вращения.
Задание 6. Сформулировать определение понятия «плечо вектора количества движения точки относительно произвольного центра».
Задание 7. Записать формулу для определения работы силы тяжести.
Задание 8. Записать формулы, выражающие принцип Даламбера для несвободной неизменяемой механической системы в координатной форме.
Задание 9. Сформулировать определение понятия «возможное перемещение системы».
Задание 10. Записать формулу, выражающую принцип возможных перемещений в векторной форме.
Практическая часть
Задание 1

Задание 2
Задание 3

Задание 4

Задание 5
Билет № 5
Теоретическая часть
Задание 1. Записать основное уравнение динамики несвободной материальной точки в векторном виде.
Задание 2. Сформулировать определение понятия «циклическая частота свободных колебаний точки».
Задание 3. Сформулировать определение понятия «внутренние силы».
Задание 4. Записать формулу для определения главного вектора реакций внешних связей.
Задание 5. Сформулировать теорему Штейнера.
Задание 6. Записать теорему импульсов в векторной форме.
Задание 7. Сформулировать определение понятия «работа постоянной силы на прямолинейном перемещении точки её приложения».
Задание 8. Записать формулу для определения силы инерции материальной точки.
Задание 9. Сформулировать определение понятия «возможная (элементарная) работа силы».
Задание 10. Записать уравнение Лагранжа второго рода.
Практическая часть
Задание 1

Задание 2
Задание 3


Задание 4
Задание 5
Билет № 6
Теоретическая часть
Задание 1 Записать дифференциальные уравнения движения несвободной материальной точки в декартовой системе отсчёта.
Задание 2. Сформулировать определение понятия «период свободных колебаний точки».
Задание 3. Записать уравнение вынужденных колебаний большой частоты.
Задание 4. Сформулировать определение понятия «несвободная механическая система».
Задание 5. Что является мерой инертности при вращательном движении твёрдого тела?
Задание 6. Записать формулу для определения импульса равнодействующей нескольких сил, действующих на точку.
Задание 7. Сформулировать определение понятия «кинетический момент механической системы относительно оси».
Задание 8. Записать формулу для определения кинетической энергии механической системы.
Задание 9. Сформулировать определение понятия «возможные перемещения несвободной механической системы».
Задание 10. Записать формулу для определения возможной работы.

Практическая часть
Задание 1

Задание 2

Задание 3

Задание 4
Задание 5
Билет № 7
Теоретическая часть
Задание 1. Записать дифференциальные уравнения движения несвободной материальной точки в естественных координатных осях.
Задание 2. Записать уравнения затухающих колебаний точки.
Задание 3. Записать уравнение вынужденных колебаний большой частоты.
Задание 4. Сформулировать определение понятия «внутренние силы».
Задание 5. Сформулировать определение понятия «момент инерции тела относительно оси вращения».
Задание 6. Записать теорему импульсов в векторной форме.
Задание 7. Записать в скалярном виде формулу, выражающую теорему об изменении кинетического момента механической системы относительно координатных осей.
Задание 8. Записать формулу, выражающую теорему об изменении кинетической энергии механической системы.
Задание 9. Сформулировать определение понятия «связи».
Задание 10. Записать формулу для определения возможной работы сил, приложенных к механической системе.
Практическая часть

Задание 1
Задание 2
Задание 3

Задание 4

Задание 5
Билет № 8
Теоретическая часть
Задание 1. Сформулировать суть первой задачи динамики.
Задание 2. Сформулировать определение понятия «период затухающих колебаний точки».
Задание 3. Записать условие, при котором происходит явление резонанса.
Задание 4. Сформулировать определение понятия «неизменяемая механическая система».
Задание 5. Что характеризует момент инерции тела относительно оси вращения?
Задание 6. Записать теорему импульсов в скалярной форме.
Задание 7. Сформулировать следствия из теоремы об изменении кинетического момента механической системы относительно координатных осей.
Задание 8. Сформулировать определение понятия «сила инерции».
Задание 9. Сформулировать определение понятия «мощность силы».
Задание 10. Сформулировать определение понятия «идеальные связи».
Практическая часть
Задание 1

Задание 2
Задание 3
Задание 4

Задание 5
Билет № 9
Теоретическая часть
Задание 1. Сформулировать суть второй задачи динамики.
Задание 2. Сформулировать определение понятия «амплитуда затухающих колебаний точки».
Задание 3. Записать дифференциальное уравнение движения точки, происходящее под действием восстанавливающей силы, возмущающей силы, изменяющейся по периодическому закону, и силы сопротивления движению, пропорциональной первой степени скорости.
Задание 4. Сформулировать определение понятия «центр масс механической системы».
Задание 5. Сформулировать теорему Штейнера.
Задание 6. Сформулировать определение понятия «количество движения механической системы».
Задание 7. Записать дифференциальные уравнения поступательного движения твёрдого тела в пространстве.
Задание 8. Записать формулу для определения силы инерции материальной точки.
Задание 9. Сформулировать определение понятия «стационарные связи».
Задание 10. Сформулировать принцип возможных перемещений.
Практическая часть
Задание 1

Задание 2
Задание 3


Задание 4
Задание 5

Билет № 10
Теоретическая часть
Задание 1. Как определяются постоянные интегрирования при решении второй задачи динамики?
Задание 2. Сформулировать определение понятия «циклическая частота затухающих колебаний».
Задание 3. Записать основное уравнение динамики относительного движения точки.
Задание 4. Записать формулу для определения радиус-вектора центра масс механической системы.
Задание 5. Записать формулу для определения момента инерции тела относительно вертикальной оси вращения.
Задание 6. Записать теорему об изменении количества движения механической системы в векторной форме.
Задание 7. Записать дифференциальное уравнение вращательного движения твёрдого тела относительно вертикальной оси.
Задание 8. Записать формулу, выражающую принцип Даламбера для несвободной материальной точки в векторной форме.
Задание 9. Записать формулы для определения инерционных нагрузок при плоскопараллельном движении твёрдого тела.
Задание 10. Сформулировать определение понятия «обобщённая скорость».
Практическая часть
Задание 1

Задание 2
Задание 3
Задание 4
Задание 5
Билет № 11
Теоретическая часть
Задание 1. Сформулировать определение понятия «восстанавливающая сила».
Задание 2. Сформулировать определение понятия «амплитуда затухающих колебаний точки».
Задание 3. Записать формулу для определения переносной силы инерции.
Задание 4. Записать формулу для определения главного вектора активных сил.
Задание 5. Сформулировать определение «радиус инерции твёрдого тела относительно оси вращения».
Задание 6. Записать теорему об изменении количества движения механической системы в скалярной форме.
Задание 7. Записать дифференциальные уравнения плоскопараллельного движения твёрдого тела.
Задание 8. Записать формулы, выражающие принцип Даламбера для несвободной материальной точки в координатной форме.
Задание 9. Записать формулы, выражающие принцип Даламбера для несвободной неизменяемой механической системы в координатной форме.
Задание 10. Записать формулу, выражающую принцип возможных перемещений в координатной форме.
Практическая часть
Задание 1

Задание 2
Задание 3
Задание 4
Задание 5
Билет № 12
Теоретическая часть
Задание 1. Сформулировать определение понятия «коэффициент жёсткости пружины».
Задание 2. Под действием каких сил происходят вынужденные колебания материальной точки?
Задание 3. Записать формулу для определения кориолисовой силы инерции.
Задание 4. Записать формулу для определения главного вектора реакций внешних связей.
Задание 5. Записать формулу для определения момента инерции механической системы.
Задание 6. Сформулировать следствия из теоремы об изменении количества движения механической системы.
Задание 7. Сформулировать определение понятия «работа постоянной силы на прямолинейном перемещении точки её приложения».
Задание 8. Записать формулы, выражающие принцип Даламбера для несвободной материальной точки в координатной форме.
Задание 9. Сформулировать определение понятия «возможная (элементарная) работа силы».
Задание 10. Записать формулу, выражающую принцип возможных скоростей (принцип возможных мощностей).
Практическая часть
Задание 1
Задание 2

Задание 3

Задание 4
Задание 5

Билет № 13
Теоретическая часть
Задание 1. Записать формулу для определения модуля силы упругости пружины.
Задание 2. Какие колебания называют колебаниями с малым сопротивлением внешней среды?
Задание 3. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть неравномерное вращение относительно неподвижной оси, а относительное движение прямолинейное.
Задание 4. Записать формулу для определения главного вектора реакций внутренних связей.
Задание 5. Сформулировать теорему о движении центра масс механической системы.
Задание 6. Сформулировать определение понятия «момент количества движения точки относительно произвольного центра».
Задание 7. Сформулировать определение понятия «элементарная работа переменной силы».
Задание 8. Записать формулы, выражающие принцип Даламбера для несвободной механической системы в векторной форме.
Задание 9. Записать формулу для определения возможной работы сил, приложенных к механической системе.
Задание 10. Сформулировать общее уравнение динамики.
Практическая часть
Задание 1
Задание 2
Задание 3

Задание 4
Задание 5
Билет № 14
Теоретическая часть
Задание 1. Под действием каких сил осуществляются свободные колебания точки?
Задание 2. Записать уравнения апериодического движения точки.
Задание 3. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть равномерное вращение относительно неподвижной оси, а относительное движение прямолинейное.
Задание 4. Записать формулу для определения вектора скорости центра масс механической системы.
Задание 5. Записать векторную формулу, выражающую теорему о движении центра масс механической системы.
Задание 6. Сформулировать определение понятия «плечо вектора количества движения точки относительно произвольного центра».
Задание 7. Записать уравнение вынужденных колебаний малой частоты.
Задание 8. Записать формулы, выражающие принцип Даламбера для несвободной неизменяемой механической системы в координатной форме.
Задание 9. Записать формулу, выражающую общее уравнение динамики в векторной форме.
Задание 10. Сформулировать определение понятия «обобщённая сила».
Практическая часть
Задание 1
Задание 2
Задание 3

Задание 4

Задание 5
Билет № 15
Теоретическая часть
Задание 1. Записать дифференциальное уравнение свободных колебаний точки.
Задание 2. Под действием каких сил происходят вынужденные колебания материальной точки?
Задание 3. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть поступательное неравномерное криволинейное движение, а относительное движение прямолинейное.
Задание 4. Записать формулу для определения вектора ускорения центра масс механической системы.
Задание 5. Записать дифференциальные уравнения движения центра масс механической системы в декартовой системе отсчёта.
Задание 6. Сформулировать определение понятия «момент количества движения точки относительно оси».
Задание 7. Сформулировать определение понятия «мощность силы».
Задание 8. Записать формулу для определения главного вектора сил инерции поступательно движущегося твёрдого тела.
Задание 9. Записать формулу для определения возможной работы сил, приложенных к механической системе.
Задание 10. Записать формулу, выражающую общее уравнение динамики в скалярной форме.
Практическая часть
Задание 1
Задание 2

Задание 3
Задание 4
Задание 5
Билет № 16
Теоретическая часть
Задание 1. Записать уравнения свободных колебаний точки.
Задание 2. Сформулировать определение понятия «период затухающих колебаний точки».
Задание 3. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть прямолинейное и равномерное движение, а относительное движение прямолинейное.
Задание 4. Записать формулы для определения проекций вектора скорости центра масс механической системы на координатные оси.
Задание 5. Сформулировать первое следствие из теоремы о движении центра масс механической системы.
Задание 6. Записать формулы для определения моментов количества движения точки относительно координатных осей.
Задание 7. Сформулировать определение понятия «кинетическая энергия».
Задание 8. Записать формулы, по которым определяются центробежная и вращательная силы инерции и момент сил инерции при вращательном движении тела относительно оси, не проходящей через центр масс, в случае, когда силы инерции приложены в центре масс.
Задание 9. Записать формулу, выражающую принцип возможных перемещений в координатной форме.
Задание 10. Записать формулу, выражающую общее уравнение динамики в координатной форме.
Практическая часть
Задание 1

Задание 2
Задание 3
Задание 4

Задание 5
Билет № 17
Теоретическая часть
Задание 1. Сформулировать определение понятия «амплитуда свободных колебаний точки».
Задание 2. Сформулировать определение термина «инерциальная система отсчёта».
Задание 3. Сформулировать принцип относительности классической механики.
Задание 4. Записать формулы для определения проекций вектора ускорения центра масс механической системы на координатные оси.
Задание 5. Сформулировать второй закон динамики (закон пропорциональности силы и ускорения).
Задание 6. Сформулировать второе следствие из теоремы о движении центра масс механической системы.
Задание 7. Записать в векторной форме формулу, выражающую теорему об изменении момента количества движения материальной точки.
Задание 8. Записать формулу для определения кинетической энергии материальной точки.
Задание 9. Записать формулу для определения момента сил инерции при вращении тела относительно оси, проходящей через его центр масс.
Задание 10. Сформулировать определение понятия «идеальные связи».
Практическая часть
Задание 1
Задание 2

Задание 3
Задание 4

Задание 5
Билет № 18
Теоретическая часть
Задание 1. Сформулировать определение понятия «период свободных колебаний точки».
Задание 2. Записать формулу для определения периода возмущающей силы.
Задание 3. Сформулировать определение понятия «механическая система».
Задание 4. Записать формулу для определения модуля скорости центра масс механической системы.
Задание 5. Сформулировать первый закон динамики (закон инерции).
Задание 6. Сформулировать определение понятия «количество движения материальной точки».
Задание 7. Записать в скалярном виде формулу, выражающую теорему об изменении момента количества движения материальной точки.
Задание 8. Записать формулу для определения кинетической энергии поступательно движущегося твёрдого тела.
Задание 9. Записать формулы для определения инерционных нагрузок при плоскопараллельном движении твёрдого тела.
Задание 10. Записать формулу, выражающую принцип возможных скоростей (принцип возможных мощностей).
Практическая часть
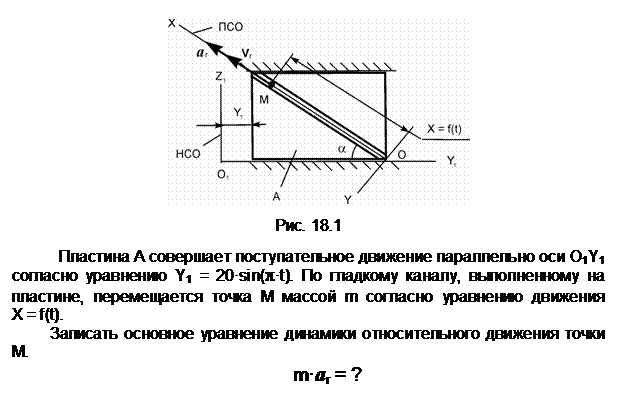
Задание 1
Задание 2
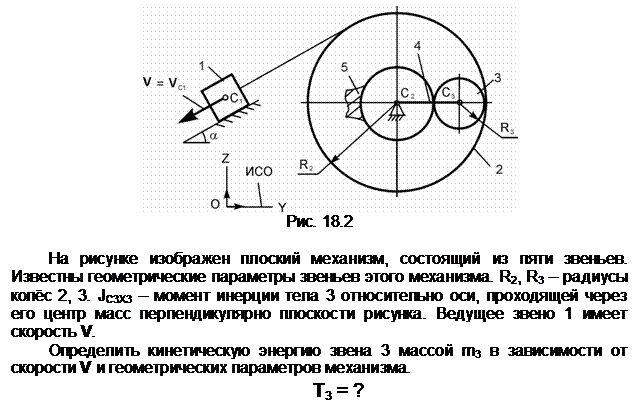
Задание 3
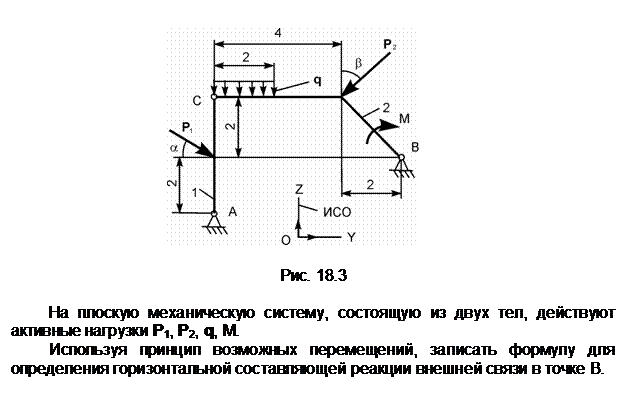
Задание 4

Задание 5
Билет № 19
Теоретическая часть
Задание 1. Сформулировать определение понятия «циклическая частота свободных колебаний точки».
Задание 2. Записать дифференциальное уравнение движения точки под действием восстанавливающей и возмущающей сил.
Задание 3. Сформулировать определение понятия «свободная механическая система».
Задание 4. Записать формулу для определения модуля ускорения центра масс механической системы.
Задание 5. Сформулировать определение понятия «импульс силы за промежуток времени».
Задание 6. Сформулировать определение понятия «центральная сила».
Задание 7. Записать формулу для определения кинетической энергии вращающегося тела относительно вертикальной оси.
Задание 8. Сформулировать определение понятия «обобщённые координаты механической системы».
Задание 9. Сформулировать определение понятия «возможная (элементарная) работа силы».
Задание 10. Сформулировать принцип возможных перемещений.
Практическая часть

Задание 1
Задание 2
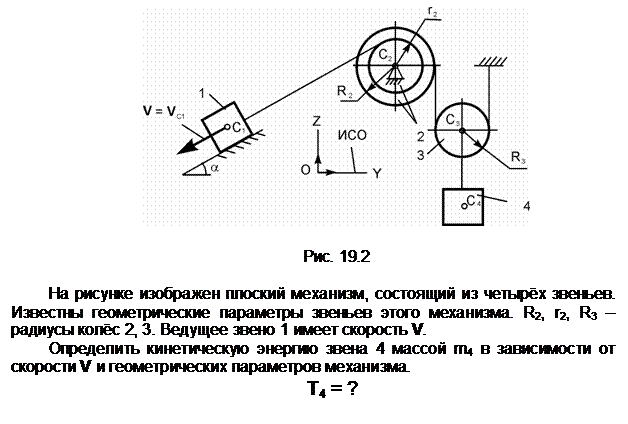

Задание 3
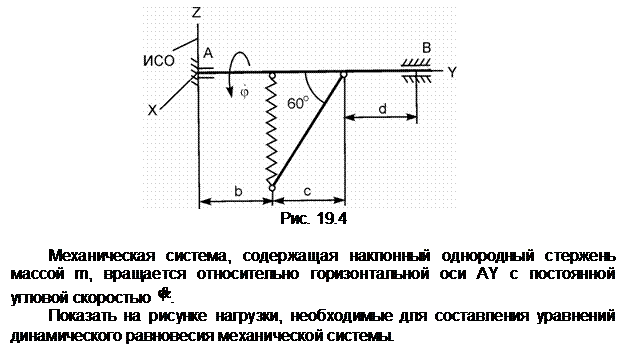
Задание 4
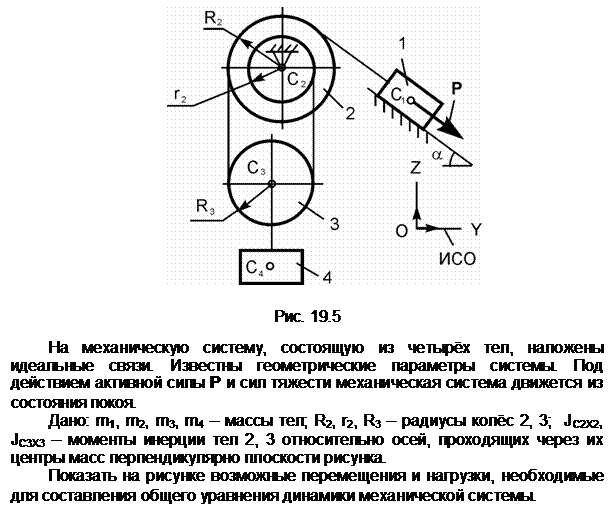
Задание 5
Билет № 20
Теоретическая часть
Задание 1. Записать дифференциальное уравнение затухающих колебаний точки.
Задание 2. Записать уравнение вынужденных колебаний малой частоты.
Задание 3. Сформулировать определение понятия «несвободная механическая система».
Задание 4. Что является мерой инертности при поступательном движении твёрдого тела?
Задание 5. Записать формулу для определения импульса силы за промежуток времени.
Задание 6. Сформулировать определение понятия «кинетический момент механической системы относительно оси».
Задание 7. Записать формулу для определения кинетической энергии механической системы.
Задание 8. Что изучает аналитическая механика?
Задание 9. Сформулировать определение понятия «возможная (элементарная) работа силы».
Задание 10. Сформулировать определение понятия «обобщённая сила».
Практическая часть
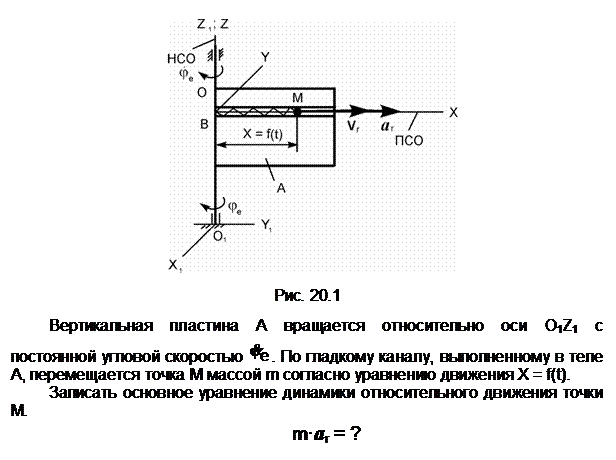
Задание 1
Задание 2

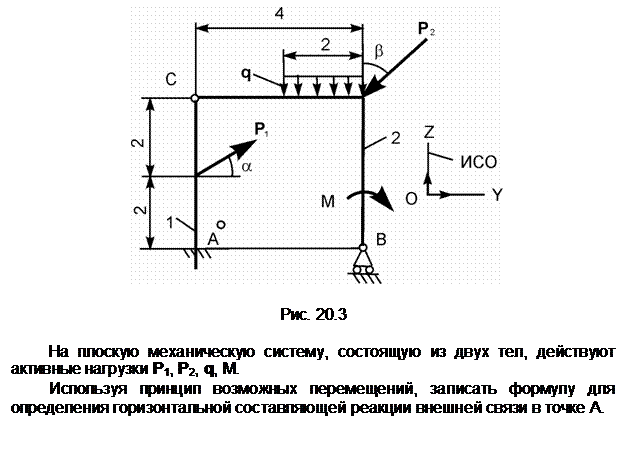
Задание 3

Задание 4
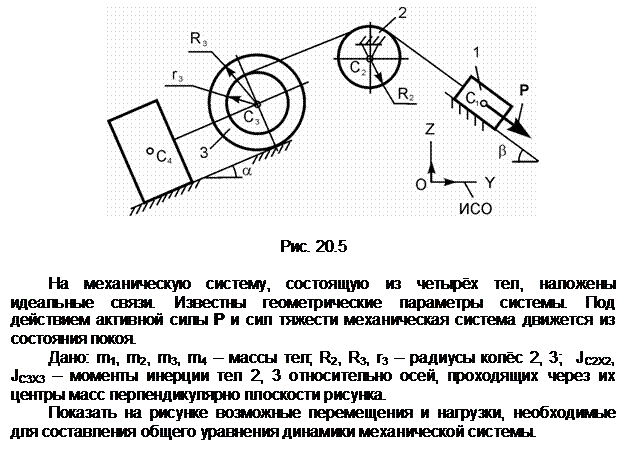
Задание 5
Билет № 21
Теоретическая часть
Задание 1. Сформулировать второй закон динамики (закон пропорциональности силы и ускорения).
Задание 2. Сформулировать определение понятия «период свободных колебаний точки».
Задание 3. Записать формулу для определения периода возмущающей силы.
Задание 4. Сформулировать определение понятия «механическая система».
Задание 5. Что является мерой инертности при вращательном движении твёрдого тела?
Задание 6. Сформулировать определение понятия «количество движения материальной точки».
Задание 7. Записать формулу для определения кинетической энергии поступательно движущегося твёрдого тела.
Задание 8. Записать формулу для определения момента сил инерции при вращении тела относительно оси, проходящей через его центр масс.
Задание 9. Сформулировать общее уравнение динамики.
Задание 10. Записать формулу, выражающую общее уравнение динамики в скалярной форме.
Практическая часть

Задание 1

Задание 2
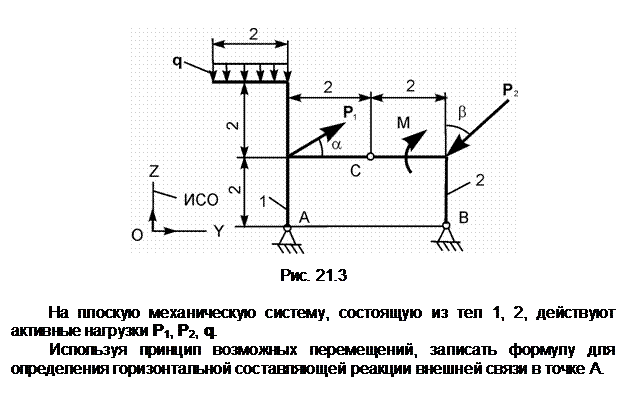
Задание 3
Задание 4
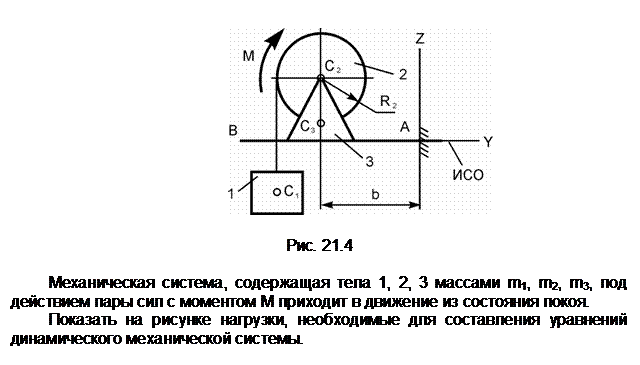
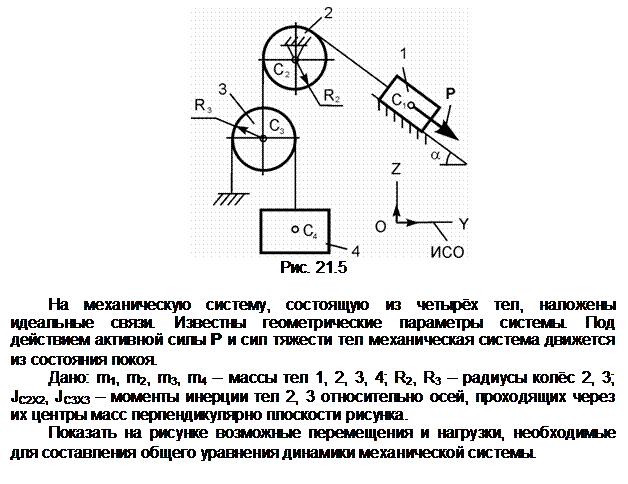
Задание 5
Билет №22
Теоретическая часть
Задание 1. Сформулировать третий закон динамики (закон равенства действия и противодействия).
Задание 2. Записать уравнения апериодического движения точки.
Задание 3. Записать формулу для определения переносной силы инерции.
Задание 4. Записать формулу для определения вектора ускорения центра масс механической системы.
Задание 5. Сформулировать второе следствие из теоремы о движении центра масс механической системы.
Задание 6. Сформулировать определение понятия «момент количества движения точки относительно оси».
Задание 7. Записать формулу для определения главного вектора сил инерции поступательно движущегося твёрдого тела.
Задание 8. Записать теорему об изменении количества движения механической системы в векторной форме.
Задание 9. Записать дифференциальные уравнения поступательного движения твёрдого тела в пространстве.
Задание 10. Сформулировать первый закон динамики (закон инерции).
Практическая часть
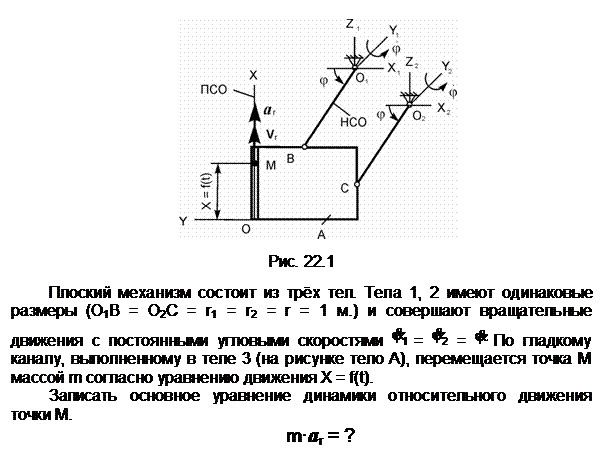
Задание 1

Задание 2
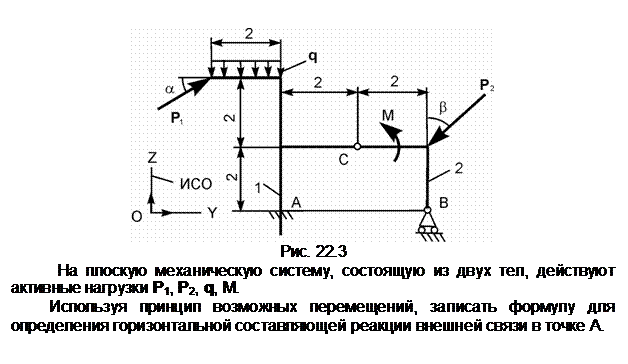
Задание 3

Задание 4

Задание 5
Билет № 23
Теоретическая часть
Задание 1. Сформулировать третий закон динамики (закон равенства действия и противодействия).
Задание 2. Под действием каких сил происходят вынужденные колебания материальной точки?
Задание 3. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть поступательное неравномерное криволинейное движение, а относительное движение прямолинейное.
Задание 4. Что является мерой инертности при поступательном движении твёрдого тела?
Задание 5. Сформулировать второе следствие из теоремы о движении центра масс механической системы.
Задание 6. Сформулировать определение понятия «центральная сила».
Задание 7. Сформулировать определение понятия «кинетическая энергия».
Задание 8. Сформулировать определение понятия «возможные перемещения несвободной механической системы».
Задание 9. Что изучает аналитическая механика?
Задание 10. Сформулировать определение понятия «обобщённая сила».
Практическая часть
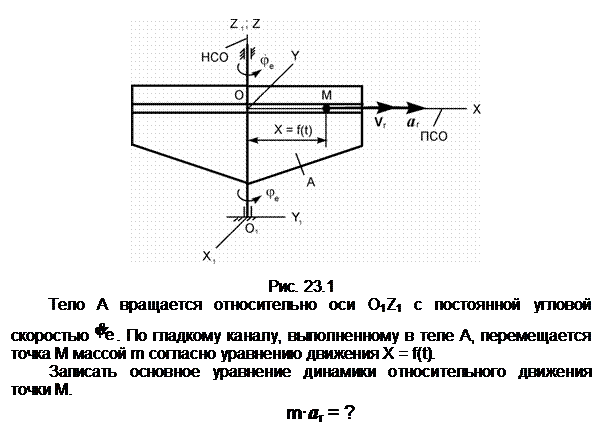
Задание 1
Задание 2
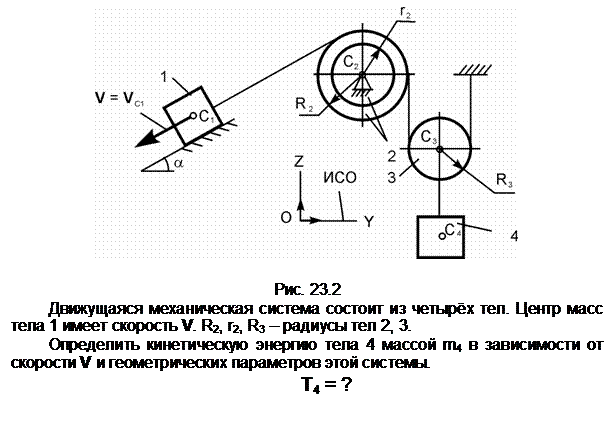
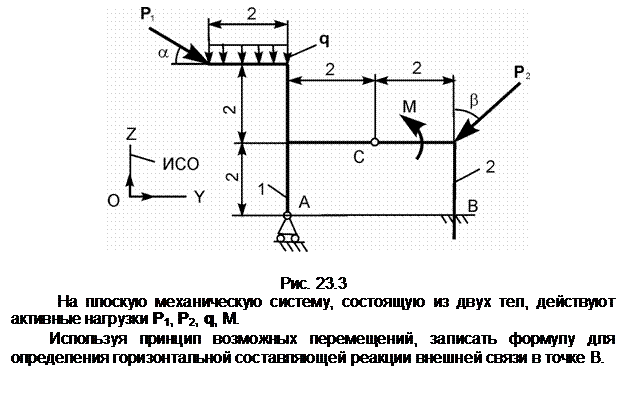
Задание 3
Задание 4
Задание 5
Билет № 24
Теоретическая часть
Задание 1. Сформулировать определение понятия «инерциальная система отсчёта».
Задание 2. Под действием каких сил происходят вынужденные колебания материальной точки?
Задание 3. Записать дифференциальное уравнение движения точки, происходящее под действием восстанавливающей силы, возмущающей силы, изменяющейся по периодическому закону, и силы сопротивления движению, пропорциональной первой степени скорости.
Задание 4. Что является мерой инертности при поступательном движении твёрдого тела?
Задание 5. Записать формулу для определения момента инерции тела относительно вертикальной оси вращения.
Задание 6. Сформулировать определение понятия «плечо вектора количества движения точки относительно произвольного центра».
Задание 7. Записать формулу для определения работы силы тяжести.
Задание 8. Записать формулы, выражающие принцип Даламбера для несвободной неизменяемой механической системы в координатной форме.
Задание 9. Сформулировать определение понятия «возможное перемещение системы».
Задание 10. Записать формулу, выражающую принцип возможных перемещений в векторной форме.
Практическая часть
Задание 1

Задание 2
Задание 3
Задание 4

Задание 5
Билет № 25
Теоретическая часть
Задание 1. Записать основное уравнение динамики несвободной материальной точки в векторном виде.
Задание 2. Сформулировать определение понятия «циклическая частота свободных колебаний точки».
Задание 3. Сформулировать определение понятия «внутренние силы».
Задание 4. Записать формулу для определения главного вектора реакций внешних связей.
Задание 5. Сформулировать теорему Штейнера.
Задание 6. Записать теорему импульсов в векторной форме.
Задание 7. Сформулировать определение понятия «работа постоянной силы на прямолинейном перемещении точки её приложения».
Задание 8. Записать формулу для определения силы инерции материальной точки.
Задание 9. Сформулировать определение понятия «возможная (элементарная) работа силы».
Задание 10. Записать уравнение Лагранжа второго рода.
Практическая часть

Задание 1
Задание 2
Задание 3

Задание 4
Задание 5
Билет № 26
Теоретическая часть
Задание 1 Записать дифференциальные уравнения движения несвободной материальной точки в декартовой системе отсчёта.
Задание 2. Сформулировать определение понятия «период свободных колебаний точки».
Задание 3. Записать уравнение вынужденных колебаний большой частоты.
Задание 4. Сформулировать определение понятия «несвободная механическая система».
Задание 5. Что является мерой инертности при вращательном движении твёрдого тела?
Задание 6. Записать формулу для определения импульса равнодействующей нескольких сил, действующих на точку.
Задание 7. Сформулировать определение понятия «кинетический момент механической системы относительно оси».
Задание 8. Записать формулу для определения кинетической энергии механической системы.
Задание 9. Сформулировать определение понятия «возможные перемещения несвободной механической системы».
Задание 10. Записать формулу для определения возможной работы.

Практическая часть
Задание 1
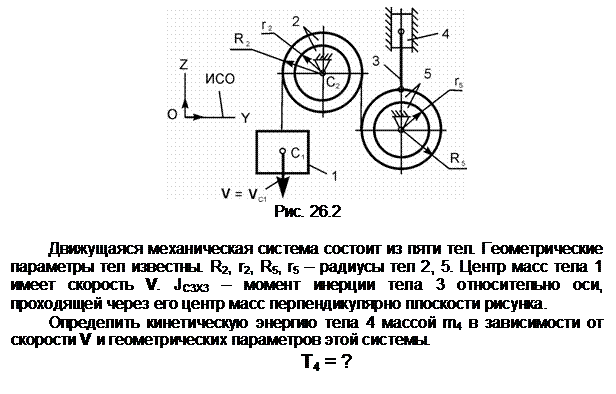
Задание 2
Задание 3
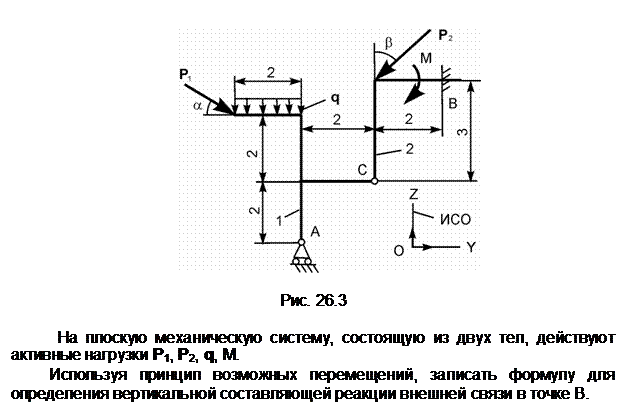

Задание 4
Задание 5
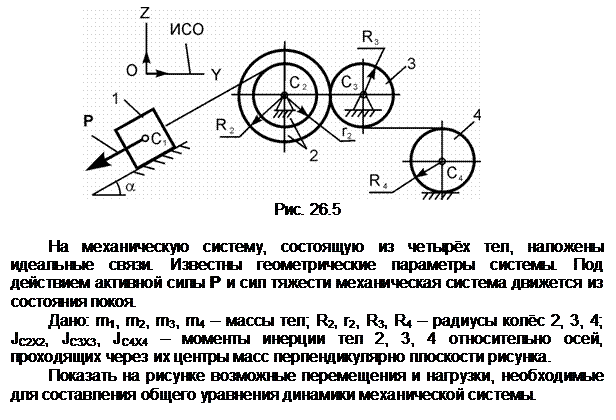
Билет № 27
Теоретическая часть
Задание 1. Записать дифференциальные уравнения движения несвободной материальной точки в естественных координатных осях.
Задание 2. Записать уравнения затухающих колебаний точки.
Задание 3. Записать уравнение вынужденных колебаний большой частоты.
Задание 4. Сформулировать определение понятия «внутренние силы».
Задание 5. Сформулировать определение понятия «момент инерции тела относительно оси вращения».
Задание 6. Записать теорему импульсов в векторной форме.
Задание 7. Записать в скалярном виде формулу, выражающую теорему об изменении кинетического момента механической системы относительно координатных осей.
Задание 8. Записать формулу, выражающую теорему об изменении кинетической энергии механической системы.
Задание 9. Сформулировать определение понятия «связи».
Задание 10. Записать формулу для определения возможной работы сил, приложенных к механической системе.
Практическая часть
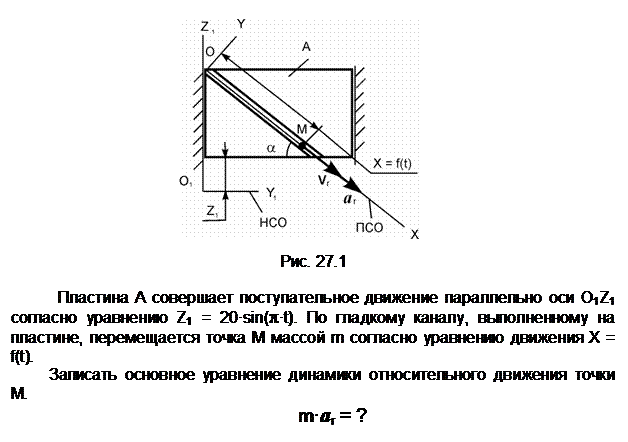
Задание 1
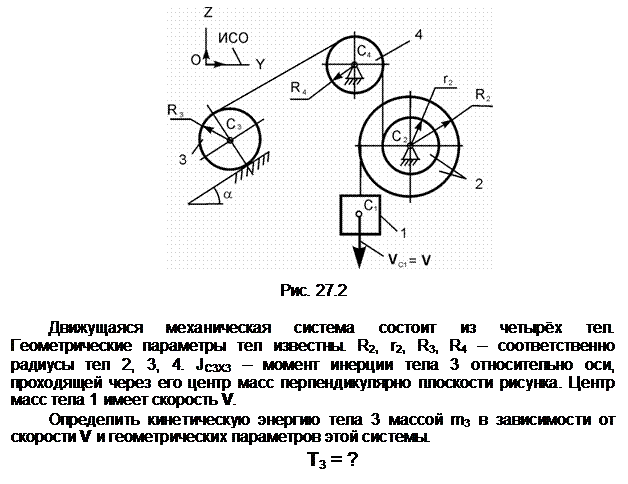
Задание 2
Задание 3
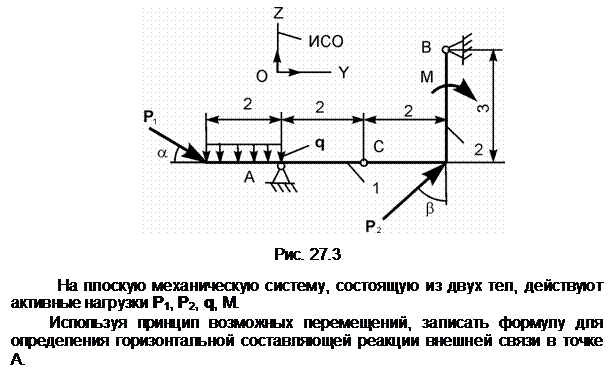

Задание 4
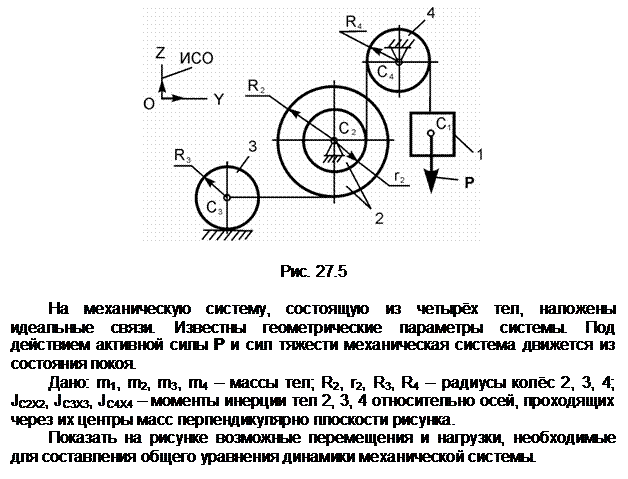
Задание 5
Билет № 28
Теоретическая часть
Задание 1. Сформулировать суть первой задачи динамики.
Задание 2. Сформулировать определение понятия «период затухающих колебаний точки».
Задание 3. Записать условие, при котором происходит явление резонанса.
Задание 4. Сформулировать определение понятия «неизменяемая механическая система».
Задание 5. Что характеризует момент инерции тела относительно оси вращения?
Задание 6. Записать теорему импульсов в скалярной форме.
Задание 7. Сформулировать следствия из теоремы об изменении кинетического момента механической системы относительно координатных осей.
Задание 8. Сформулировать определение понятия «сила инерции».
Задание 9. Сформулировать определение понятия «мощность силы».
Задание 10. Сформулировать определение понятия «идеальные связи».

Практическая часть
Задание 1

Задание 2

Задание 3
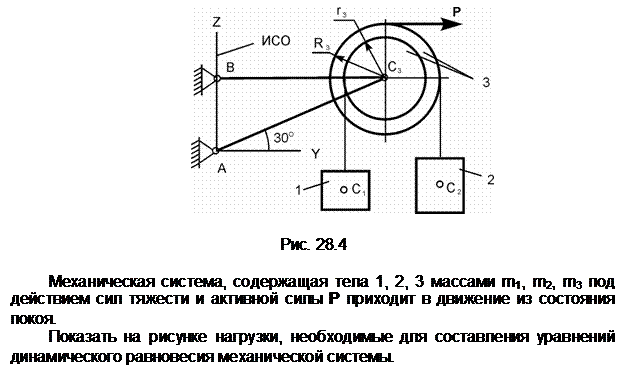
Задание 4

Задание 5
Билет № 29
Теоретическая часть
Задание 1. Сформулировать суть второй задачи динамики.
Задание 2. Сформулировать определение понятия «амплитуда затухающих колебаний точки».
Задание 3. Записать дифференциальное уравнение движения точки, происходящее под действием восстанавливающей силы, возмущающей силы, изменяющейся по периодическому закону, и силы сопротивления движению, пропорциональной первой степени скорости.
Задание 4. Сформулировать определение понятия «центр масс механической системы».
Задание 5. Сформулировать теорему Штейнера.
Задание 6. Сформулировать определение понятия «количество движения механической системы».
Задание 7. Записать дифференциальные уравнения поступательного движения твёрдого тела в пространстве.
Задание 8. Записать формулу для определения силы инерции материальной точки.
Задание 9. Сформулировать определение понятия «стационарные связи».
Задание 10. Сформулировать принцип возможных перемещений.
Практическая часть
Задание 1
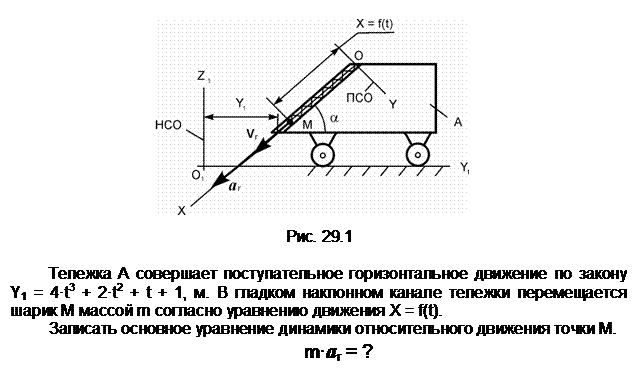

Задание 2
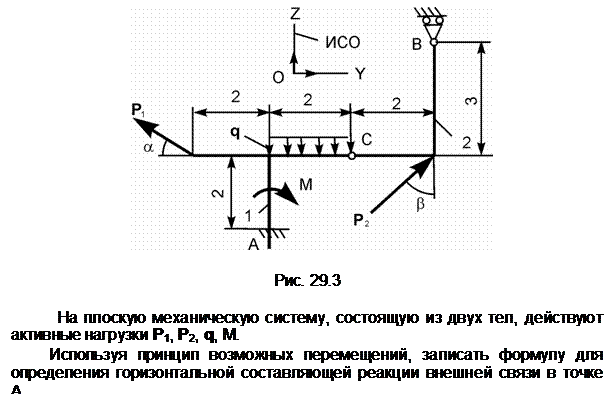
Задание 3
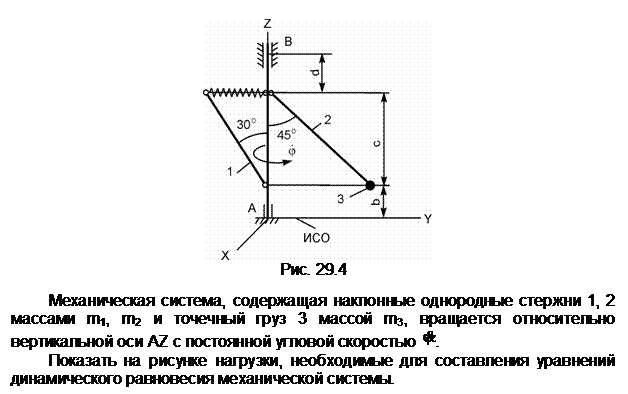
Задание 4
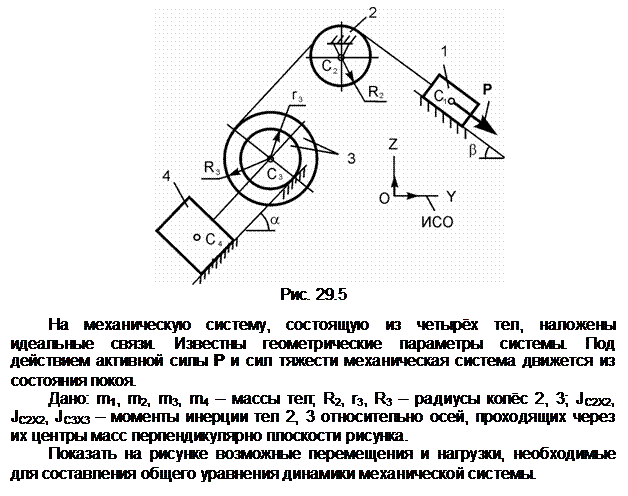
Задание 5
Билет № 30
Теоретическая часть
Задание 1. Как определяются постоянные интегрирования при решении второй задачи динамики?
Задание 2. Сформулировать определение понятия «циклическая частота затухающих колебаний».
Задание 3. Записать основное уравнение динамики относительного движения точки.
Задание 4. Записать формулу для определения радиус-вектора центра масс механической системы.
Задание 5. Записать формулу для определения момента инерции тела относительно вертикальной оси вращения.
Задание 6. Записать теорему об изменении количества движения механической системы в векторной форме.
Задание 7. Записать дифференциальное уравнение вращательного движения твёрдого тела относительно вертикальной оси.
Задание 8. Записать формулу, выражающую принцип Даламбера для несвободной материальной точки в векторной форме.
Задание 9. Записать формулы для определения инерционных нагрузок при плоскопараллельном движении твёрдого тела.
Задание 10. Сформулировать определение понятия «обобщённая скорость».
Практическая часть

Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Содержание
ВВЕДЕНИЕ…….……………………………………………………………………3
СЛОВАРЬ ТЕРМИНОВ, ОПРЕДЕЛЕНИЙ, ПОНЯТИЙ……………………….4
ВОПРОСЫ И ЗАДАНИЯ ЭКЗАМЕНАЦИОННЫХ БИЛЕТОВ..……………..11
ВАРИАНТ ЭКЗАМЕНАЦИОННЫХ БИЛЕТОВ………………..………………18
Порядок выбора экзаменационного билета………………………………18
Пример ответа на экзаменационный билет………………………………19
Теоретическая часть…………..……………………………………………..19
Практическая часть…………………………………………………………..21
Экзаменационные билеты…………………………………………………..28
Билет №1…………………………………………………………………..28
Билет №2…………………………………………………………………..31
Билет №3…………………………………………………………………..34
Билет №4…………………………………………………………………..37
Билет №5…………………………………………………………………..40
Билет №6…………………………………………………………………..43
Билет №7…………………………………………………………………..46
Билет №8…………………………………………………………………..49
Билет №9…………………………………………………………………..52
Билет №10………………………………………………………………...55
Билет №11…………………………………………………………………58
Билет №12…………………………………………………………………61
Билет №13…………………………………………………………………64
Билет №14…………………………………………………………………67
Билет №15…………………………………………………………………70
Билет №16…………………………………………………………………73
Билет №17…………………………………………………………………76
Билет №18…………………………………………………………………79
Билет №19…………………………………………………………………82
Билет №20…………………………………………………………………85
Билет №21…………………………………………………………………88
Билет №22…………………………………………………………………91
Билет №23…………………………………………………………………94
Билет №24…………………………………………………………………97
Билет №25………………………………………………………………..100
Билет №26………………………………………………………………..103
Билет №27………………………………………………………………..106
Билет №28………………………………………………………………..109
Билет №29………………………………………………………………..112
Билет №30………………………………………………………………..115
Для заметок
////////////////////////////