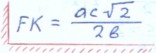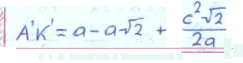поиск по сайту правообладателям
|
|
|
Общие сведения из сферической геометрии
Сфера – тело, ограниченное поверхностью, все точки которой одинаково удалены от одной точки называемой центром.
2/ Большой круг /Б.К./ – след от пересечения сферы плоскостью проходящей через центр.
3/ Малый круг /М.К./ – след от пересечения сферы плоскостью не проходящей через центр.
4/ Через две точки на поверхности сферы можно провести один Б.К. Дуга Б.К. кратчайшее расстояние на сфере между двумя точками.
5/ Сферический треугольник образуется на поверхности сферы от пересечения трех дуг Б.К.
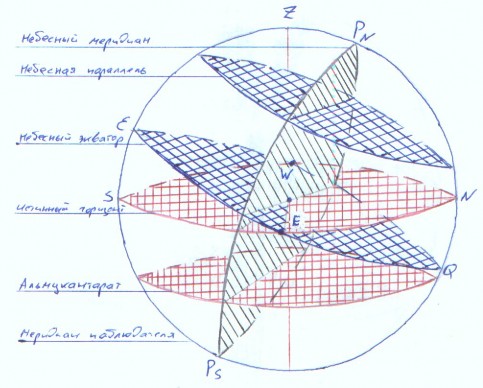
Небесная Сфера.
Небесная Сфера /Н.С./ – воображаемая сфера произвольного радиуса, на которую проектируются светила прямыми, соединяющими светила с центром сферы. Все линии и плоскости Н.С. параллельны линиям и плоскостям Земного Шара.
Основные линии и плоскости Небесной Сферы.
Отвесная линия – линия, проходящая через наблюдателя и центр Земли. Отвесная линия пересекает Н.С. в точках: верхняя – Зенит /Z/, нижняя – Надир /n/.
2/ Плоскость истинного горизонта – Б.К. перпендикулярный отвесной линии, проходящий через наблюдателя.
3/ Меридиан наблюдателя – Б.К. проходящий через Полюса мира и Зенит.
4/ Ось Мира – диаметр Н.С., параллельный оси Земли. Т.к радиус Земли несоизмеримо мал по сравнению с радиусом Н.С., то допускают, что ось Мира совпадает с осью Земли.
5/ Полюса Мира - РN, PS точки от пересечения оси Мира Сферы Небесной. 6/ Повышенный полюс – полюс находящийся в надгоризонтной части. 7/ Небесный экватор – Б.К. перпендикулярный оси Мира, проходящий через наблюдателя. Пересекает истинный горизонт в точках E и W. 8/ Надгоризонтная часть – часть небесной сферы, которая содержит N, Z, S. 9/ Подгоризонтная часть – часть небесной сферы, которая содержит N, n, S. 10/ Меридиан наблюдателя пересекает истинный горизонт в точках Севера / N/ и Юга /S/, через которые проходит полуденная линия NS.
1 Полуденная часть меридиана наблюдателя – состоит из PN, Z, PS. 12/ Полуночная часть меридиана наблюдателя - состоит из PN, n, PS. Основные круги на Небесной Сфере.
Вертикал – Б.К. проходящий через Зенит и Надир.
2/ Первый вертикал – Б.К. проходящий через Z, E, n, W.
3/ Альмуканторат – М.К. параллельный плоскости истинного горизонта. 4/ Небесный меридиан – Б.К. проходящий через полюса Мира. 5/ Небесная параллель – М.К. параллельный небесному экватору.
СФЕРИЧЕСКИЕ КООРДИНАТЫ СВЕТИЛ.
Горизонтная система координат.
Находящийся на Земле наблюдатель всегда может с помощью отвеса определить направление отвесной /вертикальной/ линии. Эта линия пересекает Н.С. в двух диаметрально противоположных точках – в Зените /Z/ – верхняя точка и в Надире /n/ – нижняя точка. Плоскость, проходящая через центр Н.С. ( а центр Н.С. есть точка на земной поверхности, где находится наблюдатель) и проведенная перпендикулярно отвесной линии пересекает Н.С. по большому кругу, который называется истинным горизонтом (в отличие от видимого горизонта).
Основные круги горизонтной системы координат: истинный горизонт и меридиан наблюдателя.
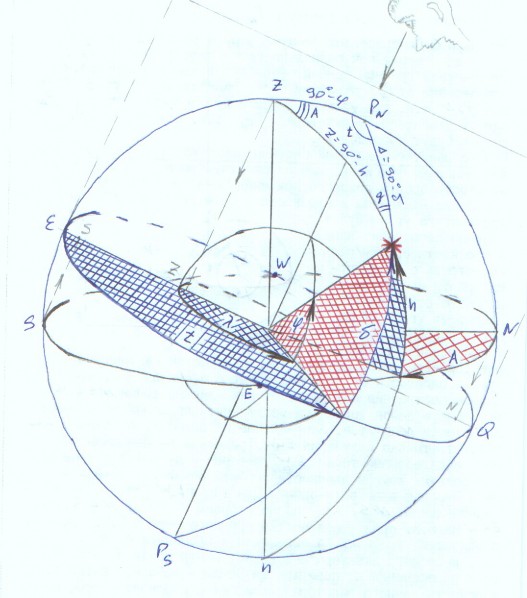
Горизонтную систему координат составляют высота и азимут.
Высота светила /h/ - угол при центре сферы между плоскостью истинного горизонта и направлением на светило, измеряется дугой вертикала светила от плоскости истинного горизонта до светила от 0 до 90.
Зенитное расстояние /z/ – дополнение высоты до 90. Измеряется дугой вертикала светила от 0 до 180 /т.к. высота светила может быть отрицательной, что означает, что светило находится под горизонтом / . (измеряется от z до светила).
Меридиональная высота /H/– максимальная высота светила в течении суток, когда светило кульминирует на меридиане наблюдателя.
Азимут светила /А/ – сферический угол при Зените, измеряется дугой истинного горизонта от меридиана наблюдателя /северной или южной половины меридиана наблюдателя/ до вертикала светила.
Полукруговой азимут /Aп/ - измеряется от точки N или S /одноимённой широтой/ к Е или W до вертикала светила. (Aп = 0 360, Aп = N100E).
Круговой азимут /Аk/ - измеряется от N по часовой стрелке. (Аk = 0 90, Аk = 80SE).
Четвертной азимут /Aч/ – измеряется от точки N или S до вертикала светила.
Горизонтная система координат удобна для определения мгновенного положения светила.
Первая экваториальная система координат.
Подобно тому как положение любой точки на земной поверхности однозначно фиксируется географическими координатами / широтой и долготой/, положение светил на Н.С. определяется экваториальными координатами – склонением и часовым углом светила/. Координатные круги первой экваториальной системы – меридиан наблюдателя и небесный экватор
Примечание: координатные круги горизонтной системы – а) истинный горизонт б) меридиан наблюдателя (связь с первой экваториальной системой)
Склонение светила // – угол при центре сферы между плоскостью небесного экватора и направлением на светило, измеряется дугой небесного меридиана между плоскостью небесного экватора и светилом.
Больное расстояние // – дополнение склонения до 90, измеряется от повышенного полюса мира.
Часовой угол светила /t/ – сферический угол при повышенном полюсе мира между полуденной частью меридиана наблюдателя и небесным меридианом светила, измеряется дугой небесного экватора от полуденной части меридиана наблюдателя в сторону W или E . Круговой часовой угол измеряется в сторону W до 360. Практический часовой угол измеряется в сторону Е или W до 180.
Вторая экваториальная система координат.
Вторую экваториальную систему координат составляют склонение // или полярное расстояние // и прямое восхождение светила.
Прямое восхождение светила // – сферический угол при повышенном полюсе мира между небесным меридианом точки Овна и небесным меридианом светила, измеряется дугой небесного экватора от меридиана точки Овна до меридиана светила в сторону обратную счета вестовых часовых углов /или в сторону годового движения Солнца/ до 360. Звездное дополнение // – = 360 -
Прямое восхождение отсчитывается вдоль небесного экватора в сторону, противоположную видимому суточному вращению Н.С. Прямое восхождение (как и долгота) выражается либо в градусах, минутах, секундах, либо в часах, минутах, секундах дуги, либо в часах, минутах, секундах времени.
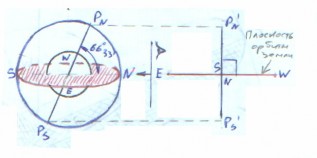
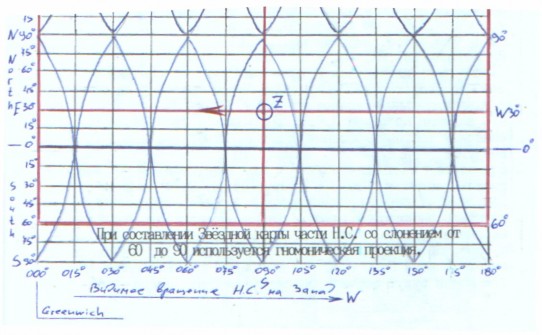
Рассмотрим вид Рис.№1 сверху - с РN, проектируя все точки на небесный экватор. Ось мира РNPS пересекает земную сферу в точке РN. Меридианы будут видны сверху как радиально расходящие прямые из РN . Проекция внешней границы земной сферы будет экватор, понятно, что направление от РN к экватору будет направление к Югу /S/ только для =N, т.к. для =S меридианы /если смотреть сверху на РN / начнут сходиться от экватора к Югу /т.к. полюса при проекции сверху будут совпадать//.
В пространстве Солнечной системы применительно к Земле, есть две основные фиксированные плоскости. Первая плоскость это плоскость орбиты годового движения Земли вокруг Солнца, т.к. ось Земли наклонена к плоскости орбиты Земли на 66 33' и плоскость этого угла будет взаимно перпендикулярна к плоскости орбиты /если посмотреть с боку /торца/ орбиты на боковую проекцию оси Земли/. Плоскость угла 66 33' будет второй основной фиксированной в пространстве плоскостью. От этих двух плоскостей /а точнее Больших кругов, плоскости которых совпадают с этими
плоскостями/ идут дальше построения которые дают нам главные точки N, S, E, W. Б.К. небесного экватора пересекает центр Земли и оставляет след пересечения на поверхности Земли – земной экватор, т.е. плоскость земного экватора совпадает с плоскостью небесного экватора и Б.К. этих плоскостей имеют общий центр /центр Земли/, поэтому угловые величины земных долгот равны угловым величинам часовых углов, которые отсчитываются от Гринвичского меридиана гринвичские часовые углы/. Аналогично, угловые величины географических широт равны угловым величинам склонений. На небесном экваторе нет точек N, S, E, W. Эти точки существуют условно, т.к. Н.С. не имеет определенного радиуса. Мы можем говорить о реально существующих точках только на поверхности сферы имеющей физическую границу. Так в астрономии есть только две конкретные точки – это полюс N и полюс S.
ВИДИМОЕ СУТОЧНОЕ ДВИЖЕНИЕ СВЕТИЛ.
При суточном вращении небосвода взаимное расположение звезд не меняется, и наблюдателю кажется, что звезды находятся на внутренней стороне огромной шаровой поверхности /сфере/. В действительности звезды движутся в пространстве, но эти движения при суточном движении незначительны и ими пренебрегают, считая, что звезды неподвижны. Небесная Сфера /Н.С./ – это воображаемая сфера сколь угодно большого радиуса, в центре которой находится глаз наблюдателя. На такую сферу и проецируют звезды, Солнце, Луну, планеты и т.д., отвлекаясь от действительных расстояний до светил и рассматривая лишь угловое расстояние между ними. Наблюдаемое суточное вращение Н.С. /оно происходит с востока на запад/ это кажущееся явление, отражающее действительное вращение земного шара вокруг , оси /с запада на восток/. Ось видимого вращения Н.С. называется осью мира . Не будет большой ошибки если считать что ось мира совпадает с земной осью /См. рис №. Более строго ось мира параллельна земной оси. Участвуя во вращении Н.С. светила описывают суточные параллели /суточная параллель – малый круг Н.С., плоскость которого перпендикулярна оси мира/. При движении по параллели светило пересекает плоскость истинного горизонта /восходит, заходит/, пересекает 1 вертикал /изменяется наименование азимутов/, пересекает Меридиан наблюдателя /нижняя и верхняя кульминация/. Характер видимого суточного движения светила зависит от широты наблюдателя и склонения светила.
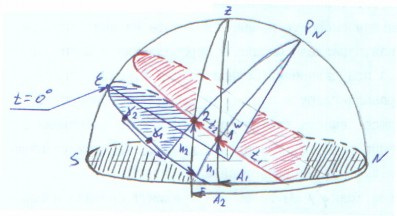
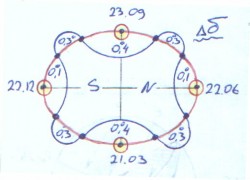
Светило восходит и заходит, если < 90 - Светило незаходящее, если > 90 - и одноимённо с . Светило не восходящее, если > 90 - и разноимённо с . Светило пересекает 1 вертикал над горизонтом, если < и одноимённо с . Светило проходит через Зенит, если = и одноимённо с . В момент верхней кульминации светила, когда оно проходит полуденную часть меридиана наблюдателя, его часовой угол t = 0, а в момент нижней кульминации t = 180.
Светило 1 : Не пересекает 1 вертикал, т.к. > , незаходящее , т.к. > 90 - и одноимённо с . Светило 2 : Пересекает 1 вертикал над горизонтом, т.к. < и одноимённо с , не заходящее , т.к. > 90 - и одноимённо с . Светило 3 : Пересекает 1 вертикал над горизонтом, т.к. < и одноимённо с , восходит и заходит, т.к. < 90 - . Светило 4 : Пересекает 1 вертикал под горизонтом, т.к. < и разноимённо с , невосходящее, т.к. > 90 - и разноимённо с . Светила 1, 2, 3, 4 не проходят через Зенит, т.к. .
Характер изменения сферических координат светил в следствии суточного движения.
Скорость вращения Земли считаем равномерной, соответственно равномерно перемещается любой небесный меридиан.
А : Изменение экваториальных координат.
а) Часовой угол в течение суток изменяется равномерно от 0 до 360. б) Склонение светила постоянно. в) Прямое восхождение постоянно (т.к. меридиан точки Овна перемещается одновременно с меридианом светила) Б : Изменение горизонтных координат.
Закон изменения высоты : h = -sin sinA t Закон изменения азимута : A = -sin + cos cosA tgh t
а) Высота светила постоянно изменяется. Закон изменения высоты тригонометрический : h = -sin sinA t У 1 вертикала изменение высоты максимальное, а около меридиана наблюдателя светило движется почти параллельно горизонту, т.е. высота почти не меняется. Наибольшая скорость изменения высоты на экваторе, т.к. суточная параллель близка к перпендикуляру истинного горизонта, а при склонении Солнца равным 0, Солнце двигается по перпендикуляру к плоскости истинного горизонта. На полюсе высота светила в течении суток неизменна. б) Изменение азимута. У меридиана наблюдателя азимут меняется быстро, а у 1 вертикала медленно.
Общий вывод : Если 90, то высота и азимут светила изменяются непрерывно и неравномерно. Если = 90 (на полюсе) высота не изменяется, а азимут изменяется равномерно. При = 0 (на экваторе) у меридиана наблюдателя азимут изменяется быстро, а у горизонта не изменяется.
ВИДИМОЕ СОБСТВЕННОЕ ГОДОВОЕ ДВИЖЕНИЕ СОЛНЦА.
В отличие от звёзд, экваториальные координаты которых остаются неизменными на протяжении многих месяцев и даже лет, есть светила, и которых быстро изменяются. К числу таких светил, которые не только участвуют (как звёзды) в суточном движении, но и совершают собственные перемещения на Н.С., относится Солнце. Видимое движение Солнца в течении года происходит по спроецированной на Н.С. эклиптике, которая наклонена по отношению к небесному экватору на 2327’. Солнце, двигаясь по эклиптике, проходит меридиан точки Овна через 365 суток 5 часов 48 минут 46 секунд. Эклиптика и небесный меридиан пересекаются в двух точках весеннего и осеннего равноденствий (в точках Овна и Весов), где изменяется наименование склонения Солнца. Наибольшей величины склонение Солнца достигает в точках летнего и зимнего солнцестояний (в точках Рака 2327’N и Козерога 2327’S). Вдоль эклиптики расположены 12 созвездий Зодиака (созвездие Змееносца к зодиакальным не относится).
Изменение склонения и прямого восхождения Солнца в следствии движения по эклиптике.
Эклиптика есть проекция годового движения Солнца на Н.С. Т.к. Земля движется по орбите против часовой стрелке (если смотреть на Северный полюс) вокруг Солнца, то и по эклиптике Солнце будет перемещаться против часовой стрелке.
Т.к. Земля движется вокруг Солнца неравномерно, видимое годовое движение Солнца по эклиптике происходит также с неравномерной скоростью. Суточное изменение долготы (эклиптическая долгота) неравномерно, соответственно неравномерно изменяется . меняется в пределах 54’ 66’, в сутки в среднем 1,0. Изменения склонения Солнца. Пределы изменения = 0’ 24’ в сутки. Быстро изменяется в дни равноденствий (0,4 в сутки, в месяц до и после точки равноденствия). В месяц до и после солнцестояния по 0,1 в сутки. В остальные месяцы по 0,3 в сутки.
Для приближенных расчетов склонения и прямого восхождения принимаем месяц равный 30 суткам. Чтобы приближенно рассчитать и на определённую дату, необходимо умножить величину суточного изменения и на количество суток от ближайшей даты равноденствия или солнцестояния и результат прибавить (отнять) значение и на выбранную ближайшую дату равноденствия или солнцестояния.
Пример : Рассчитать и на дату 20.11 Ближайшая дата зимнего солнцестояния 22.12 = 23,5S , = 270 20.11 – 22.12 = 32 суток. = (2 х 0,3 = 0,6) + (30 х 0,1 = 3,0) = 3,6 ; = 23,5 – 3,6 = 19,9S
= 32 х 1,0 = 32 ; = 270 – 32 = 238
Видимое годовое движение Солнца обуславливает смену времён года и деление поверхности Земли на климатические пояса.
Наблюдатель на экваторе = 0 День равен ночи. Солнце проходит через Зенит в дни 21.03 и 23.09. Касается 1 вертикала в дни 21.03 и 23.09. Меридиональная высота минимум 66,5 (90 – 23,5N или S), максимум 90 (Солнце в Зените). Времён года не существует. Азимут восхода / захода = 90
Наблюдатель в тропическом поясе (= 2327’ N 2327’S) День равен ночи в дни равноденствия. Проходит через Зенит в северном тропике в день летнего солнцестояния 22.06 ( = 23 27’ N), в южном тропике в день зимнего солнцестояния 22.12 ( = 23 27’ S). Пересекает 1 вертикал от 21.03 до 23.09, в южном тропике от 23.09 до 21.03 (в над горизонтной части). Меридиональная высота от 90 до 43.
Наблюдатель в умеренных широтах (2327’ N/S < > 6633’ N/S)
День равен ночи в дни равноденствий (21.03 и 23.09). В северных умеренных высотах день увеличивается с 22.12 до 22.06 дня летнего солнцестояния, самый длинный день в году, день уменьшается с 22.06 до 22.12 дня зимнего солнцестояния, самый короткий день (самая длинная ночь) в году. Солнце никогда не проходит через Зенит, т.к. широта всегда больше склонения. Пересекает первый вертикал в северных широтах в над горизонтной части от 21.03 до 23.09, в южных широтах от 23ю09 до 22ю12. Всегда Солнце восходит и заходит. Меридиональная высота максимальная на широте 23 27’ = 90 (когда склонение солнца максимальное и одноименно с широтой), минимальная на широте 66 33’ = 0 (когда склонение максимальное и разноименно с широтой). Но в умеренный пояс не входят параллели 23 27’ и 66 33’. Поэтому меридиональная высота в умеренном поясе в зависимости от широты и склонения Солнца изменяется от 0 до 90, и никогда не бывает равным 0 или 90.
Наблюдатель в полярном поясе (6633’ < < 90) В каждом полушарии полярный круг (66 33’) ограничивает вокруг полюса полярный пояс. Имеет полярная ночь и полярный день (т.е. продолжительность дня/ночи более 24 часов). День равен ночи в дни равноденствия на широтах до 90. Солнце всегда пересекает 1 вертикал, в над горизонтной части когда склонение разноимённо с широтой. Меридиональная высота максимальная на полярном круге в день солнцестояния, когда склонение Солнца максимальное и разноименное с наименованием полярного круга и составляет 0. Меридиональная высота также будет равняться 0 на любой другой широте больше 66 33’, когда будет выполняться условие (90 - ) - = 0, формула справедлива для любого склонения отличного от 23 27’ и когда склонение разноимённо с широтой.
Наблюдатель на полюсе (= 90) День и ночь длятся по полгода. На Северном полюсе полярный день начинается в день весеннего равноденствия и заканчивается в день осеннего равноденствия. Солнце никогда не проходит через Зенит. На полюсе компас не покажет направления на Север, поэтому невозможно определить стороны светы (1 вертикал совпадает с плоскостью истинного горизонта). Меридиональная высота максимальна в день солнцестояния, когда склонение максимально и одноимённо с наименованием Полюса и составляет 23 27’. Меридиональная высота минимальна в дни равноденствия и составляет 0.
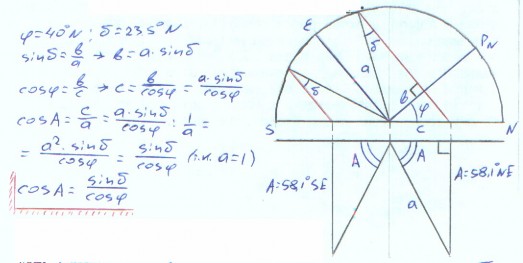
Рассмотр рисунка. Наблюдатель находится на широте 40N. Очевидно, что при любом северном склонении Солнца день будет длиннее, чем при любом южном склонении, следуя дальше этому принципу, можно сказать, что при любом склонении начиная от 23 27’ S до 23 27’ N день будет увеличиваться. При этом азимут восхода Солнца будет изменяться от ESE до ENE, при склонении 0 азимут восхода равен ровно E (азимут захода ровно W). Меридиональная высота при склонении 23,5 N равна 73,5 S , при склонении 23,5 S равна 26,5 S, поэтому при максимальной высоте Солнца солнечные лучи падают более отвесно, чем при минимальной, когда они скользят по поверхности Земли, а также день будет дольше при максимальной высоте, всё это объясняет почему температура летом больше, чем зимой.
Вид с Севера проекций видимого дневного движения Солнца. Солнце А кульминирует на меридиане наблюдателя и имеет меридиональную высоту 26,5. Рассчёт производится по формуле : Н = 90- + N - “+” S - “-“
Зная меридиональную высоту и склонение можно найти широту : = 90- Н +
Расчёт азимутов восхода и захода.
Если одноимённа с , то получаем четвертной азимут от наименования и . Если разноименно с , то получаем четвертной азимут от наименования . Полученная угловая величина отсчитывается от N или S при восходе в сторону Е и в сторону W при заходе.
,, A
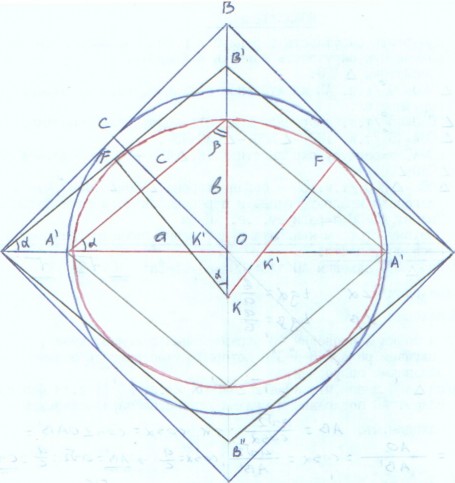
llJrn Toro, 1.1To 6b1 Hat.1ep'I'HTb 3JIJIHIIco11;:i. c 3a,uaHHblMH nonyocmm a 11 6 /rne a - 6oJibWfill nonyocb/ Heo6xo:i11Mo HaT11 pa.o.11ycb1 nsyx OKpymIOCTeH' KOTOpbIC COCTaB.RT 11CKOMblH 3JIJll1ilCOH,D,. Pa;:i.11ycb1 Haxo.ll.RT no cJ1e.nyiow,11M opJiaM :
" r .' ,,, ,,,_ , ' ''''" '
,.,
rne F K - pa.n.11yc 6onbwei1 01<py1KHOCTH A' '- pan11yc MeHbWeH oKpyJKHOCTH c - l'HI OTeHy3a npHMOyrOJibHOro TpeyrOJibHHKa c KaTeTaMl1 Cl C'f t
ДИАПАЗОН ГРИНВИЧЕСКИХ ВЕСТОВЫХ УГЛОВ.
Для того, чтобы узнать какой диапазон гринвичских вестовых углов будет виден в данный момент времени, необходимо знать гринвичское время наблюдений и долготу наблюдателя (Тгр и ). Долготу необходимо перевести гринвичский вестовый часовой угол (если долгота вестовая, то оставляем её без изменений, если восточная, то необходимо от 360 - Е) получим экваториальные координаты Зенита наблюдателя.
Если теперь от полученного tгрwz отнять и прибавить 90, то получим диапазон при Тгр = 00h. Для того, чтобы узнать диапазон на определённое Тгр , необходимо Тгр перевести в градусную меру, от tгрwz отнять Тгр при этом получим tгрwz’ (на определённое время). и от полученного tгрwz’ отнять и прибавить 90, чтобы получить диапазон на определённое Тгр. 1) tгрwz (если = W то = tгрwz , если = Е то 360 - (Е) = tгрwz) 2) Тгрh 00 00,0’ (Тгр’) 3) tгрwz - Тгр’ = tгрwz’ 4) (tгрwz’ - 90) tгрwz’ (tгрwz’ + 90)
Т.к Земля вращается вокруг своей оси в то время как Н.С. остается неподвижной, земной гринвичский меридиан нельзя использовать для координирования небесных светил, необходимо иметь какой либо фиксированный меридиан на самой Н.С. который бы при видимом суточном вращении Н.С. перемещался вместе (одновременно) с остальными небесными меридианами (светилами). За такой меридиан принимается меридиан точки Овна. Разберемся с понятием часового угла. По определению часовой угол есть сферический угол при повышенном полюсе мира между полуденной частью меридиана наблюдателя и небесным меридианом светила, измеряется дугой небесного экватора от полуденной части меридиана наблюдателя в сторону Запада. Т.к полуденная часть меридиана наблюдателя состоит из PN, Z, PS, то можно заключить, что полуденная часть меридиана наблюдателя будет являться меридианом Зенита, а как ранее было доказано гринвичский вестовый часовой угол земной долготы будет равняться гринвичскому вестовому часовому углу Зенита (при этом, естественно, небесный гринвичский меридиан будет перемещаться при суточном вращении Земли так же как и земной гринвичский меридиан). Поэтому при пользовании определением часового угла приведенного выше, нужно принимать во внимание, что этот часовой угол будет являться местным часовым углом т.к он будет отсчитываться от меридиана Зенита ( т.е. долготы наблюдателя). Т.к в определении сказано ”между полуденной частью меридиана наблюдателя ...”, то можно заключить, что Солнце (для примера) будет иметь на этом местном меридиане наивысшую высоту (меридиональную) когда, соответственно, местное время будет равно 12 часам (местный полдень).
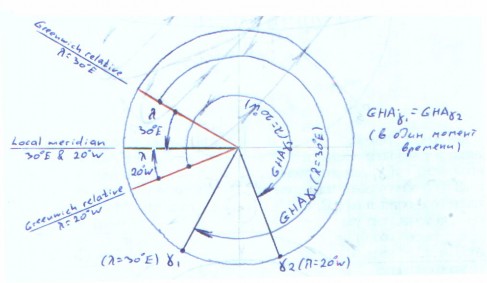
Сложнее будет происходить с небесными светилами. Рассмотрим чертеж проекции Н.С. сверху на Северный полюс на небесный экватор. Чертеж показывает относительное вращение небесных светил – Солнца и точки Овна. Для удобства, небесные параллели этих светил показаны отдельно. Видимое, вращение этих светил происходит относительно неподвижных полуденной части меридиана наблюдателя (Зенита, т.е. долготы наблюдателя), земного гринвичского меридиана и, соответственно, небесного гринвичского меридиана (так кажется земному наблюдателю, на самом деле происходит обратное : вращается Земля, а Н.С. остается неподвижной).
--.,...._ _...,':J.:19· J l I I
P1i1c .f-2
PHc •. 3
Вопрос : Какую часть Н.С. наблюдатель, находясь в точке на поверхности Земли с определенными географическими координатами, сможет наблюдать на определенный момент времени.
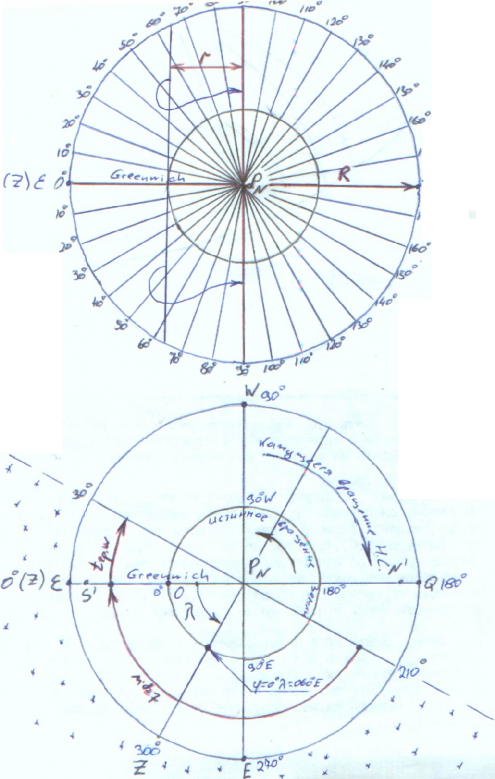
Рассмотрим Рис.2. Точка на Земле с координатами = 00 = 000 .Этой точкой будет заканчиваться проекция гринвичского меридиана (точка 0). Наблюдатель, находясь в точке 0, сможет в один момент времени наблюдать половину Н.С., т.к. взгляд наблюдателя распространяется прямолинейно и по отношению к поверхности Земли, множество взглядов, перпендикулярных отвесной линии, составят плоскость истинного горизонта (но не видимого), которая будет касаться поверхности Земли в одной точке (точке, где находится наблюдатель). Т.к. радиус Земли (r) по отношению к радиусу Н.С. (R) чрезвычайно мал, то) по отношению к радиусу Н.С. (R) чрезвычайно мал, то ) чрезвычайно мал, то можно принять, что при проекции плоскости истинного горизонта сверху, полученная касательная к поверхности Земли в точке 0, будет совпадать с параллельным диаметром Н.С. Тогда для данного случая (при = 00 = 000) наблюдатель сможет наблюдать половину Н.С. с диапазоном вестовых часовых углов от 270 до 90 через 000, т.к. в этой половине Н.С. находится Зенит, т.е. видимая часть Н.С.
Рассмотрим Рис. 3. Наблюдатель находится в точке на Земле с координатами = 00 = 060Е соответственно Зенит наблюдателя будет находиться на Н.С. с экваториальными координатами = 0 tгрwz = 300. Из рисунка видно, что видимая половина Н.С. будет находиться в диапазоне гринвичских вестовых часовых углов от 210 до 30 через 300 (часовой угол Зенита). Для этого случая, когда = 00 и соответственно = 0 наблюдатель сможет наблюдать Н.С. со склонением от 90S до 90N. Допустим, что при прежней долготе = 060Е наблюдатель будет находиться на широте = 30N. Тогда, очевидно, что наблюдатель не сможет видеть часть Н.С. со склонением ниже 60S (90 – 30), а северный полярный полюс будет все время над горизонтом на высоте равной широте 30 ,а следовательно над горизонтом все время будут светила со склонением от 90N до 60N.
ВЫВОД
Наблюдатель, находясь в точке на поверхности Земли с определенными географическими координатами и в один момент времени сможет наблюдать часть Н.С. с определенными диапазонами гринвичских вестовых часовых углов и склонений.
Диапазон гринвичских вестовых часовых углов:
t = (270 - ) через гринвичский вестовый часовой угол Зенита до (090 - ) при = E, то знак "+" ; при = W, то знак "-".
Как видно из формулы видимая половина Н.С. начинается от гринвичского вестового часового угла 270 - , и идет по ходу увеличения гринвичских вестовых часовых углов до 090 - . Для перевода географической долготы в гринвичские вестовые часовые углы необходимо:
Диапазон склонений:
Для = N, = (90S – ) вдоль меридиана наблюдателя до Северного полюса и ниже на широту наблюдателя до плоскости истинного горизонта. Т.е. Полярный полюс всегда будет находиться на высоте равной широте. По аналогии с = N формула справедлива и для = S.
To inser) по отношению к радиусу Н.С. (R) чрезвычайно мал, тоt par) по отношению к радиусу Н.С. (R) чрезвычайно мал, тоt of missing text
Относительно полуденной части меридиана наблюдателя перемещаются небесные меридианы Солнца, точки Овна и других небесных светил с Востока на Запад (видимое перемещение). Для данного примера =30Е Поэтому Солнце будет кульминировать на данной долготе на 2 часа раньше чем на меридиане Гринвича (т.к. 30 = 2h). Из этого следует, что относительно меридиана Гринвича на Востоке все моменты будут происходить раньше, т.е. время на Востоке всегда больше. Рассмотрим характер изменения экваториальной координаты – гринвичского часового угла (вестового) Солнца и точки Овна. Независимо от долготы наблюдателя, гринвичский вестовый часовой угол точки Овна и звезд, будет величина постоянная.
С течением суток Солнце будет в верхней кульминации через каждые 24 часа (строго). За эти 24 часа Солнце будет совершать суточный виток, плоскость этого витка не будет параллельна небесному экватору (в отличии от небесных параллелей звёзд). Это происходит потому, что Солнце, кроме суточного вращения (видимого) совершает еще и собственное перемещение по годовой эклиптике в сторону противоположную видимому суточному вращению на солнца = 1 (или 4 минуты).Из этого следует, что Солнце за 24 часа проходит расстояние больше, чем точка Овна и звезды на солнца (или 4 минуты), а это значит, что звездные сутки длиннее солнечных суток на 4 минуты. Солнечные (истинные) сутки – промежуток времени между двумя последовательными нижними кульминациями Солнца.
Звёздные сутки – промежуток времени между двумя последовательными верхними кульминациями точки Овна на данном меридиане наблюдателя.
Гринвичский вестовый часовой угол точки Овна ежедневно на одно и тоже время увеличивается на величину солнца = 54’ 66’ ( 1 или 4 минуты).
ВРЕМЯ
Для измерения времени используются естественные периодические процессы, в частности движение Земли по Орбите, вращение Земли вокруг своей оси, собственные колебания молекул и атомов определённых веществ. Звёздные сутки – промежуток времени между двумя последовательными верхними кульминациями точки Овна на данном меридиане наблюдателя. Промежуток времени от последней верхней кульминации точки Овна (принимается за начало звёздных суток) до данного момента называется звёздным временем S. которое равно часовому углу точки Овна, т.е. S = t, выражается обычно в градусной мере и даты не имеет.
Основная формула звёздного времени. Для любого светила (для любой точки на Н.С.) с часовым углом t* и прямым восхождением * справедлива основная формула времени : S = t* + *
Отсюда, добавляя к S 360 и заменяя * звёздным дополнением * = 360-*, получим формулу для расчета местных вестовых часовых углов точки Овна : t= S + *
В разные периоды года начало звёздных суток приходится на разное время дня и ночи и поэтому в повседневной жизни звёздное время не применяется (звездные сутки длиннее солнечных на 4 минуты).
///////////////////////////////////
|
|
|